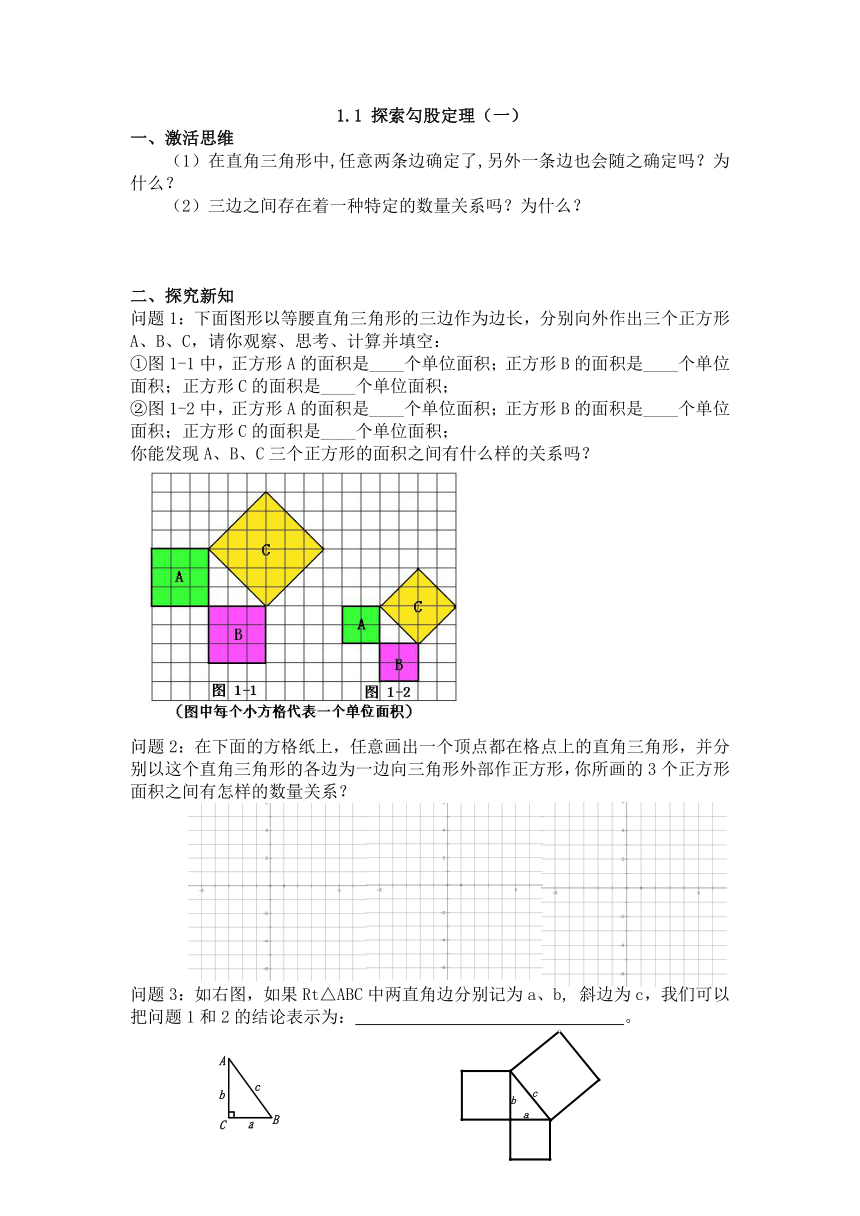
1.1 探索勾股定理(一) 一、激活思维 (1)在直角三角形中,任意两条边确定了,另外一条边也会随之确定吗?为 什么? (2)三边之间存在着一种特定的数量关系吗?为什么? 二、探究新知 问题 1:下面图形以等腰直角三角形的三边作为边长,分别向外作出三个正方形 A、B、C,请你观察、思考、计算并填空: ①图 1-1 中,正方形 A的面积是____个单位面积;正方形 B的面积是____个单位 面积;正方形 C的面积是____个单位面积; ②图 1-2 中,正方形 A的面积是____个单位面积;正方形 B的面积是____个单位 面积;正方形 C的面积是____个单位面积; 你能发现 A、B、C三个正方形的面积之间有什么样的关系吗? 问题 2:在下面的方格纸上,任意画出一个顶点都在格点上的直角三角形,并分 别以这个直角三角形的各边为一边向三角形外部作正方形,你所画的 3个正方形 面积之间有怎样的数量关系? 问题 3:如右图,如果 Rt△ABC 中两直角边分别记为 a、b, 斜边为 c,我们可以 把问题 1和 2的结论表示为: 。 � � A c b cb C a B a 小结:直角三角形两直角边的平方和等于斜边的平方。这就是著名的勾股定理, 其中:条件是_____,结论是_____.我国古代把直角三角形 较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”。 三、双基巩固 例 1:如图,在下列横线上填上适当的值: x= , y= , n= 四、综合运用 例 2:如图,在△ABC 中,∠BAC=90°,AB=6,AC=8,AD⊥BC,垂足为 D,求 BC,AD 的长. 五、分层反馈 �� �1.求下图中字母所代表的正方形的面积。 81 A 225 B 225 400 A=_____ B=_____ 2.已知:如图,在△ABC 中,AB=13,AC=20,AD=12,且 AD⊥BC,垂足为点 D,求 BC 的长. 3.如图,求等腰三角形 ABC 的面积. 4.(★)如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中 最大的正方形的边长是 8cm,则图中的所有的正方形的面积之和是 . 1.1 探索勾股定理(二) 一、激活思维 勾股定理 � 图形 定理条件 定理结论 直接应用 在 Rt △ ABC 中 , A a=40,b=9, c b 则c2 = C a B 二、探究新知 问题探究:如图是用硬纸板做成的四个全等的直角三角形(两直角边长分别是 a, b,斜边长为 c)和一个边长为 c的正方形,请你将它们拼成一个能证明勾股定 理的图形,并利用此图形证明勾股定理. 方法 1:利用 4个全等的直角三角形拼出了右图的大正方形。 证明:从整体看,大正方形面积可以表示为: , 如果分为五个部分来看, 又可以表示为: + + + + c2 则: = 因此: 方法 2:利用同样的 4个全等的直角三角形拼出了右图的正方形。 证明:从整体看,大正方形面积可以表示为: , 如果分为五个部分来看, 又可以表示为: + + + + (b-a)2 则: = 因此: 三、双基巩固 例 1:如图,飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶上方 4000 米处,过了 20 秒,飞机距离这个男孩头顶 5000 米。飞机每秒飞行多少米? 四、综合运用 例 2:观察右图,用数格子的方法判断图中三角形的三边长是否满足 a +b =c 在图(1)中 a,b,c 满足的关系式是: 它是 三角形。 在图(2)中 a,b,c 满足的关系式是: 它是 三角形。 五、分层反馈 1.一个直角三角形的斜边长为 20cm,且两直角边的长度比为 3:4,求两直角边 长。 2.如图,要修建一个育苗棚,棚高 h=1.8m,棚宽 a=2.4m,棚的长为 12m,现 要在棚顶上覆盖塑料薄膜,试求需要多少平方米塑料薄膜? 3.(★)(1)如图 1是一个重要公式的几何解释,请你写出这个公式; (2)伽菲尔德(1881 年任美国第 20 届总统)利用(1)中的公式和图 2证明了 勾股定理(1876 年 4 月 1 日发表在《新英格兰教育日志》上),现请你尝试证明 2 2 2 过程.说明:c=a +b . 1.2 一定是直角三 ... ...
~~ 您好,已阅读到文档的结尾了 ~~