24.3.2圆内接四边形 同步练习（含答案）

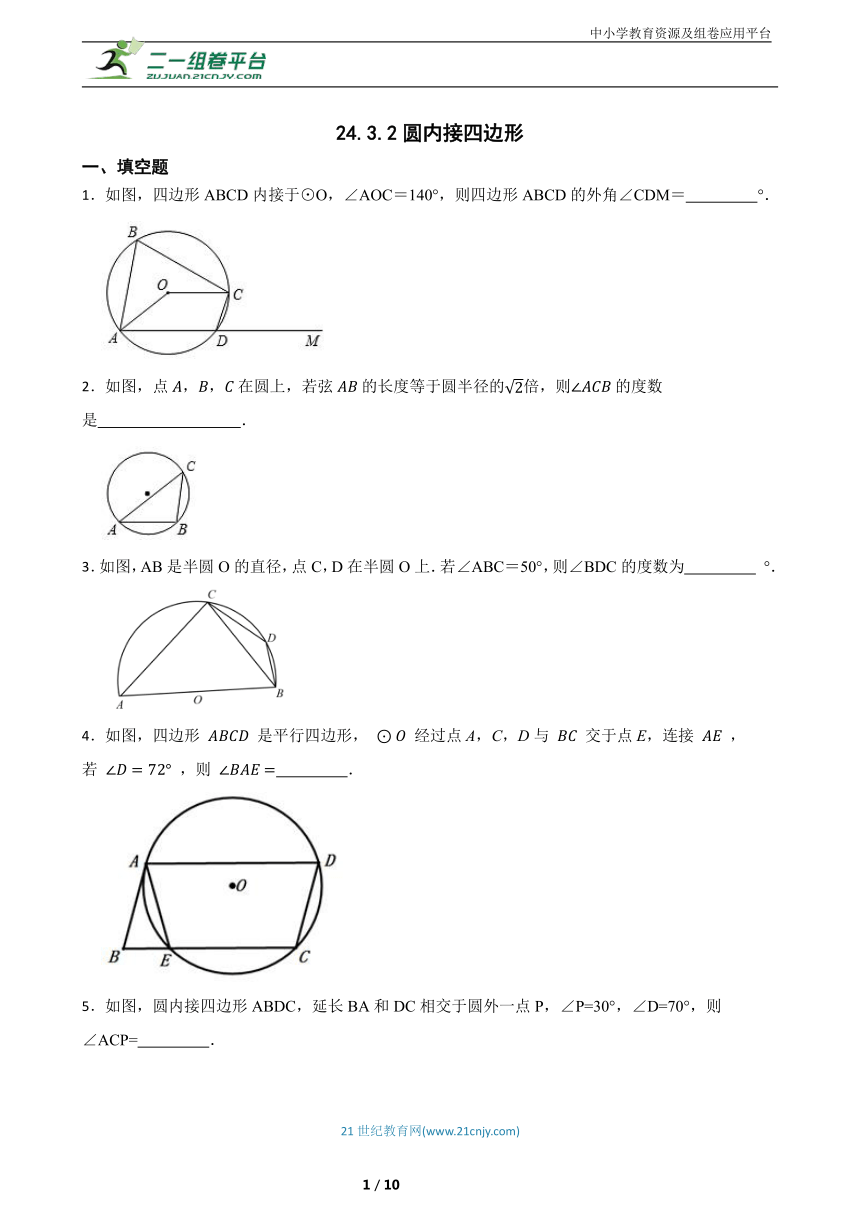
中小学教育资源及组卷应用平台 24.3.2圆内接四边形 一、填空题 1．如图，四边形ABCD内接于⊙O，∠AOC＝140°，则四边形ABCD的外角∠CDM＝　 　°． 2．如图，点，，在圆上，若弦的长度等于圆半径的倍，则的度数是　 　． 3．如图，AB是半圆O的直径，点C，D在半圆O上．若∠ABC＝50°，则∠BDC的度数为　 　 °． 4．如图，四边形 是平行四边形， 经过点A，C，D与 交于点E，连接 ，若 ，则 　 　． 5．如图，圆内接四边形ABDC，延长BA和DC相交于圆外一点P，∠P=30°，∠D=70°，则∠ACP=　 　． 6．如图，在等边三角形ABC中，点D，E分别是边BC，CA上的点，且BD=CE，连结AD，BE交于点P．连接CP，若CP⊥AP时，则AE：CE=　 　；设△ABC的面积为S1，四边形CDPE的面积为S2，则＝　 　． 二、单选题 7．如图，四边形 为 的内接四边形，若 ，则 等于（　　） A． B． C． D． 8．如图，四边形内接于，，，则的半径为（　　） A．4 B． C． D． 9．如图，在⊙O中，点A，B，C在⊙O上，且∠ACB＝100°，则∠α＝（　　） A．80° B．100° C．120° D．160° 10．如图，四边形内接于，在延长线上，若，则的度数是（　　） A． B． C． D． 11．如图，点A，B，C均在⊙上，当时，的度数是（　　） A．100° B．110° C．120° D．130° 12．如图，⊙C过原点，且与两坐标轴分别交于点A，点B，点A的坐标为（0，3），M是第三象限内 上一点，∠BMO=120°，则⊙C的半径长为（　　） A．6 B．5 C．3 D． 13．如图，四边形ABCD内接于⊙O，DA=DC，∠CBE=50°，则∠DAC的大小为（　　） A．130° B．100° C．65° D．50° 14．若四边形ABCD是⊙O的内接四边形，且∠A：∠B：∠C=1：3：8，则∠D的度数是（　　） A．10° B．30° C．80° D．120° 15．如图， 是半圆O的直径，点C，D在半圆O上．若 ，则 的度数为（　　） A． B． C． D． 16．如图， 已知中， 直径于点H， 点D在上， 且，过点A作于点E， 已知的周长为， 且， 则的半径长为（ ） A． B． C． D． 三、解答题 17．（1）如图1，是的直径，C、D是上的两点，若，，求 ①的度数 ②的度数 （2）如图2，的弦垂直平分半径，若的半径为4，求弦的长． 18．如图，四边形ABCD是⊙O的内接四边形，若∠BOD=88°，求∠BCD的度数. 19．如图，为的直径，，为上两点，，连接，，，，过点作交的延长线于点． （1）求证：直线是的切线； （2）若，，求，的长． 20．如图，四边形ABCD内接于⊙O，∠BAD=90°， = ，过点C作CE⊥AD，垂足为E，若AE=3，DE= ，求∠ABC的度数． 四、计算题 21．如图，四边形ABCD内接于⊙O，E为AB延长线上一点，若∠AOC＝150°，求∠EBC的度数． 答案解析部分 1．【答案】70． 【知识点】圆内接四边形的性质 2．【答案】或 【知识点】圆周角定理；圆内接四边形的性质 3．【答案】140 【知识点】圆周角定理；圆内接四边形的性质 4．【答案】36° 【知识点】圆内接四边形的性质 5．【答案】80° 【知识点】圆内接四边形的性质 6．【答案】2； 【知识点】三角形全等及其性质；圆内接四边形的性质；相似三角形的判定与性质；直角三角形斜边上的中线 7．【答案】C 【知识点】圆内接四边形的性质 8．【答案】B 【知识点】圆周角定理；圆内接四边形的性质 9．【答案】D 【知识点】圆周角定理；圆内接四边形的性质 10．【答案】A 【知识点】圆内接四边形的性质 11．【答案】D 【知识点】圆周角定理；圆内接四边形的性质 12．【答案】C 【知识点】圆周角定理；圆内接四边形的性质 13．【答案】C 【知识点】圆内接四边形的性质 14．【答案】D 【知识点】圆内接四边形的性质 15．【答案】D 【知识点】圆周角定理；圆内接四边形的性质 16．【答案】D 【知识点】等腰三角形的判定与性质；勾股定理 ... ...