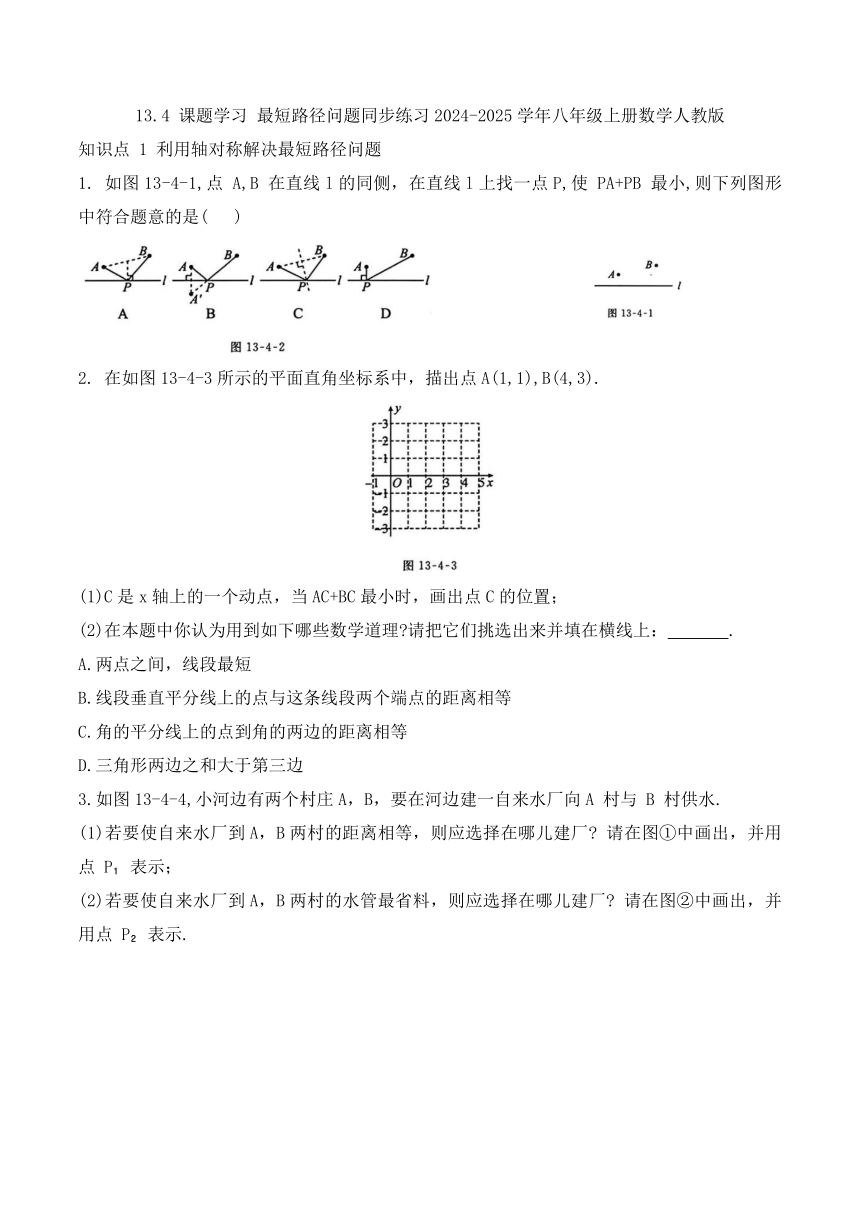
13.4 课题学习 最短路径问题同步练习2024-2025学年八年级上册数学人教版 知识点 1 利用轴对称解决最短路径问题 1. 如图13-4-1,点 A,B 在直线l的同侧,在直线l上找一点P,使 PA+PB 最小,则下列图形中符合题意的是( ) 2. 在如图13-4-3所示的平面直角坐标系中,描出点A(1,1),B(4,3). (1)C是x轴上的一个动点,当AC+BC最小时,画出点C的位置; (2)在本题中你认为用到如下哪些数学道理 请把它们挑选出来并填在横线上: . A.两点之间,线段最短 B.线段垂直平分线上的点与这条线段两个端点的距离相等 C.角的平分线上的点到角的两边的距离相等 D.三角形两边之和大于第三边 3.如图13-4-4,小河边有两个村庄A,B,要在河边建一自来水厂向A 村与 B 村供水. (1)若要使自来水厂到A,B两村的距离相等,则应选择在哪儿建厂 请在图①中画出,并用点 P 表示; (2)若要使自来水厂到A,B两村的水管最省料,则应选择在哪儿建厂 请在图②中画出,并用点 P 表示. 4.如图13-4-5,在锐角∠AOB内有一定点 P,试分别在OA,OB 上确定点 C,D,使△PCD的周长最短.(保留作图痕迹,不写作法) 5. 如图 13-4-6,△ABC 是等边三角形,AD 是BC 边上的高,E是AC 的中点,P 是AD 上的一个动点,当 PC+PE 最小时,求∠ACP 的度数. 知识点 2 利用平移法解决最短路径问题 6. 如图13-4-7,A,B两地在一条河的两岸,现要在河上造一座桥 MN,使从A 到 B的路径AMNB 最短的是图13-4-8中的(假定河的两岸是平行的直线,桥要与河岸垂直) ( ) 如图13-4-9,P,Q 两村之间隔着两条河,需要架设两座桥,桥与河岸垂直.设两条河的宽度相同且保持不变,则桥建在何处才能使两村之间的路程最短 (保留作图痕迹,不写作法) P 8. 如图13-4-10,在四边形 ABCD中,∠A=∠C=90°,M,N 分别是 BC,AB 边上的动点,∠B=56°,当△DMN 的周长最小时,∠MDN 的度数是 ( ) A.124° B.68° C.60° D.56° 9. 如图13-4-11,在平面直角坐标系中,点 M,N的坐标分别为(1,4)和(3,0),Q是y 轴上的一个动点,且M,N,Q三点不在同一直线上,当△MNQ 的周长最小时,点Q 的坐标是 10. 如图13-4-12,某公路(可视为x轴)的同一侧有A,B,C三个村庄,要在公路边建一货栈D,向A,B,C三个村庄送农用物资,路线是 D→A→B→C→D或D→C→B→A→D.在公路边是否存在一点 D,使送货路线之和最短 若存在,请在图中画出点 D 的位置,并简要说明作法;若不存在,请说明理由. 11.如图13-4-13,两个居民小区A 和 B 在河岸l的同侧,现欲在河岸边建一个长度为s米的绿化带 CD,使C到小区 A 的距离与 D 到小区 B 的距离之和最小.请在图中画出绿化带的位置.(保留作图痕迹,不写作法) 12. 如图13-4-14,小华每天都要去李奶奶家,在途中她要先到草场打一捆草,再到林区捡一捆柴,然后到达李奶奶家,最后回家.她选择怎样的路线才能使行程最短 (保留作图痕迹,不写作法) ... ...
~~ 您好,已阅读到文档的结尾了 ~~