第五章 平行四边形 2 平行四边形的判定 第1课时 平行四边形的判定（1）（含答案）

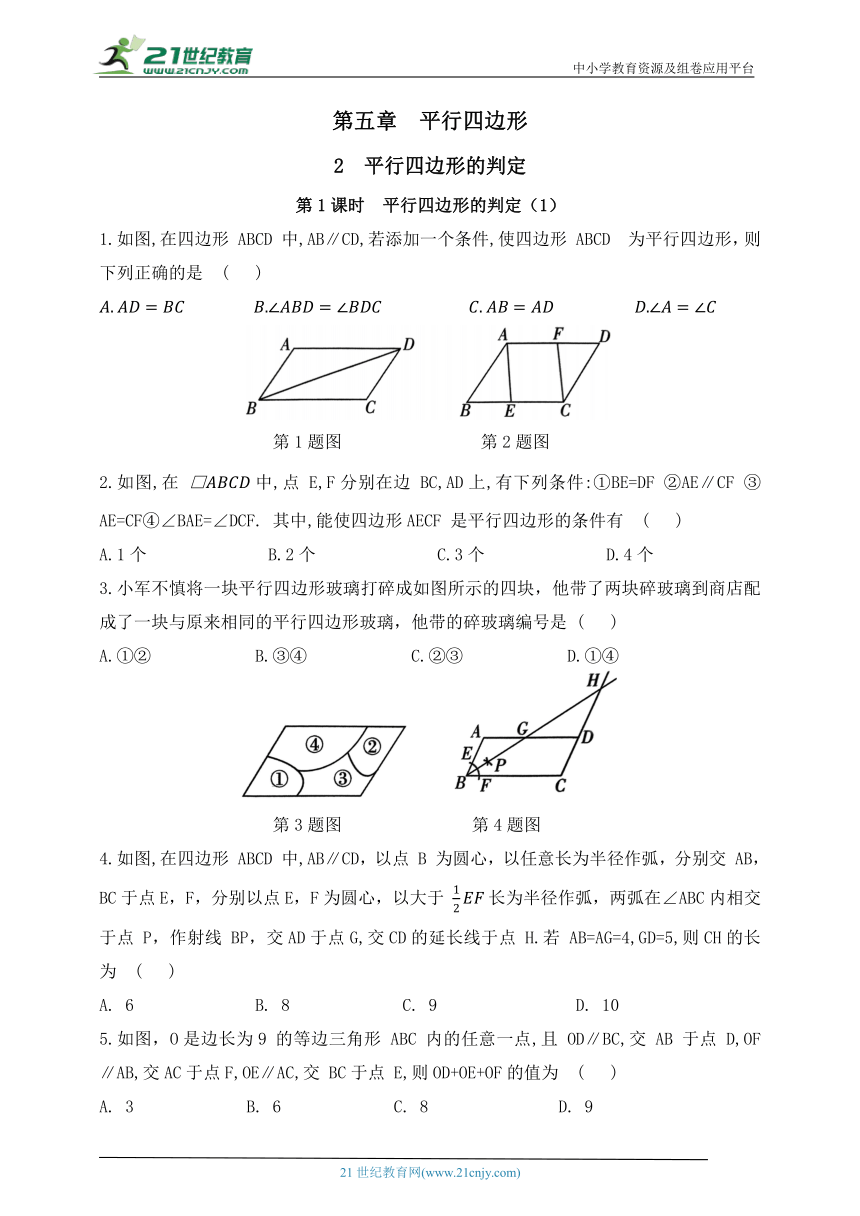
中小学教育资源及组卷应用平台 第五章 平行四边形 2 平行四边形的判定 第1课时 平行四边形的判定（1） 1.如图,在四边形 ABCD 中,AB∥CD,若添加一个条件,使四边形 ABCD 为平行四边形，则下列正确的是 ( ) 第1题图 第2题图 2.如图,在 中,点 E,F分别在边 BC,AD上,有下列条件:①BE=DF ②AE∥CF ③AE=CF④∠BAE=∠DCF. 其中,能使四边形AECF 是平行四边形的条件有 ( ) A.1个 B.2个 C.3个 D.4个 3.小军不慎将一块平行四边形玻璃打碎成如图所示的四块，他带了两块碎玻璃到商店配成了一块与原来相同的平行四边形玻璃，他带的碎玻璃编号是 ( ) A.①② B.③④ C.②③ D.①④ 第3题图 第4题图 4.如图,在四边形 ABCD 中,AB∥CD，以点 B 为圆心，以任意长为半径作弧，分别交 AB，BC于点E，F，分别以点E，F为圆心，以大于 长为半径作弧，两弧在∠ABC内相交于点 P，作射线 BP，交AD于点G,交CD的延长线于点 H.若 AB=AG=4,GD=5,则CH的长为 ( ) A. 6 B. 8 C. 9 D. 10 5.如图，O是边长为9 的等边三角形 ABC 内的任意一点,且 OD∥BC,交 AB 于点 D,OF∥AB,交AC于点F,OE∥AC,交 BC于点 E,则OD+OE+OF的值为 ( ) A. 3 B. 6 C. 8 D. 9 第5 题图 第6题图 6.如图,在△ABC中, AB=6,AC=8,BC=10,△ABD,△ACE,△BCF 都是等边三角形，下列结论：①AB⊥AC ②∠DFE=135°③四边形 AEFD是平行四边形 ④四边形 AEFD 的面积为20.其中所有正确的序号是 ( ) A.①② B.①③ C.②④ D.③④ 7.在四边形 ABCD中,已知,要使四边形 ABCD为平行四边形，则边 AD的长应为_____ cm. 8.如图,以△ABC的顶点 A为圆心，以BC长为半径B作弧；再以顶点 C 为圆心，以AB长为半径作弧，两弧相交于点 D，连接AD，CD，则四边形 ABCD 是平行四边形的依据是_____；若∠B=65°,则∠D 的大小是_____. 第8题图 第9题图 9.如图，在四边形ABCD中, ∥将AB,CD 分别平移到 EF 和 EG 的位置，若 则FG的长为_____. 10.如图所示，在 中,E,F,G,H分别在四条边上，且 那么EF与GH 互相平分吗 为什么 11.如图,在中,AF 平分 交 BC 于点F,CE平分 交AD 于点E. (1)若 求CF 的长; (2)连接BE,与AF相交于点G,连接DF,与CE相交于点 H,求证:EF 和GH 互相平分. 12.已知:如图,在四边形ABCD中, BD 垂直平分AC,垂足为 E, AC, (1)求证：四边形 ABDF 是平行四边形； (2)如果 求四边形ABCD 的面积. 13.在 中，AC,点 D 在边 BC 所在的直线上,过点 D 作 ∥交直线AB 于点 F, ∥交直线AC 于点 E.若 则 参考答案 1. D 2. C 3. B 4. C 5. D 6. B 7.2 8.两组对边分别相等的四边形是平行四边形 9.3 10.解:EF 与GH 互相平分,理由: 连接EH,HF,FG,GE,如图所示: ∵四边形ABCD 是平行四边形， ∴AD-DH=BC-BG,即AH=CG, 在△AEH 和△CFG中, ∴△AEH≌△CFG(SAS),∴EH=FG, 同理,得 HF=EG, ∴四边形 EHFG是平行四边形，∴EF与GH 互相平分. 11.解:(1)∵四边形ABCD 是平行四边形, ∥∠BCD,∠ABF=∠CDE,AB=CD,∴∠DAF=∠AFB, ∵AF平分∠BAD, (2) 证明: AF 平分∠BAD,CE平分∠BCD, ∴∠BAF=∠DAF=∠FCE=∠DCE, ∵∠DAF=∠AFB,∴∠FCE=∠AFB,∴AF∥CE, 在□ABCD中,AE∥CF,∴四边形AFCE 是平行四边形， ∴AE=CF,∴DE=BF, ∵AB=CD,∠BAE=∠DCF,∴△BAE≌△DCF(SAS),∴BE=DF, ∴四边形 BFDE是平行四边形，∴BE∥DF, ∵AF∥CE,∴四边形 EGFH 是平行四边形，∴EF和GH 互相平分. 12.解:(1)证明:∵BD垂直平分AC,∴AB=CB,AD=CD, ∴∠BAC=∠BCA,∠DAC=∠DCA,∴∠BAC+∠DAC=∠BCA+∠DCA,即∠DAB=∠BCD, ∵∠BCD=90°,AD⊥DF,∴∠DAB=∠BCD=∠ADF=90°,∴AB∥DF, ∵BD⊥AC,AF⊥AC,∴AF∥BD,∴四边形 ABDF 是平行四边形； (2)∵∠ADF=90°,AF=10,DF=6, ∵四边形ABDF是平行四边形，∴AB=DF,AF=DB, 在△ADF和△DAB中, ∴△ADF≌△DAB(SSS), 同理，得 13.2或12 解析:如图1 ... ...