第五章 平行四边形 3 三角形的中位线（含答案）

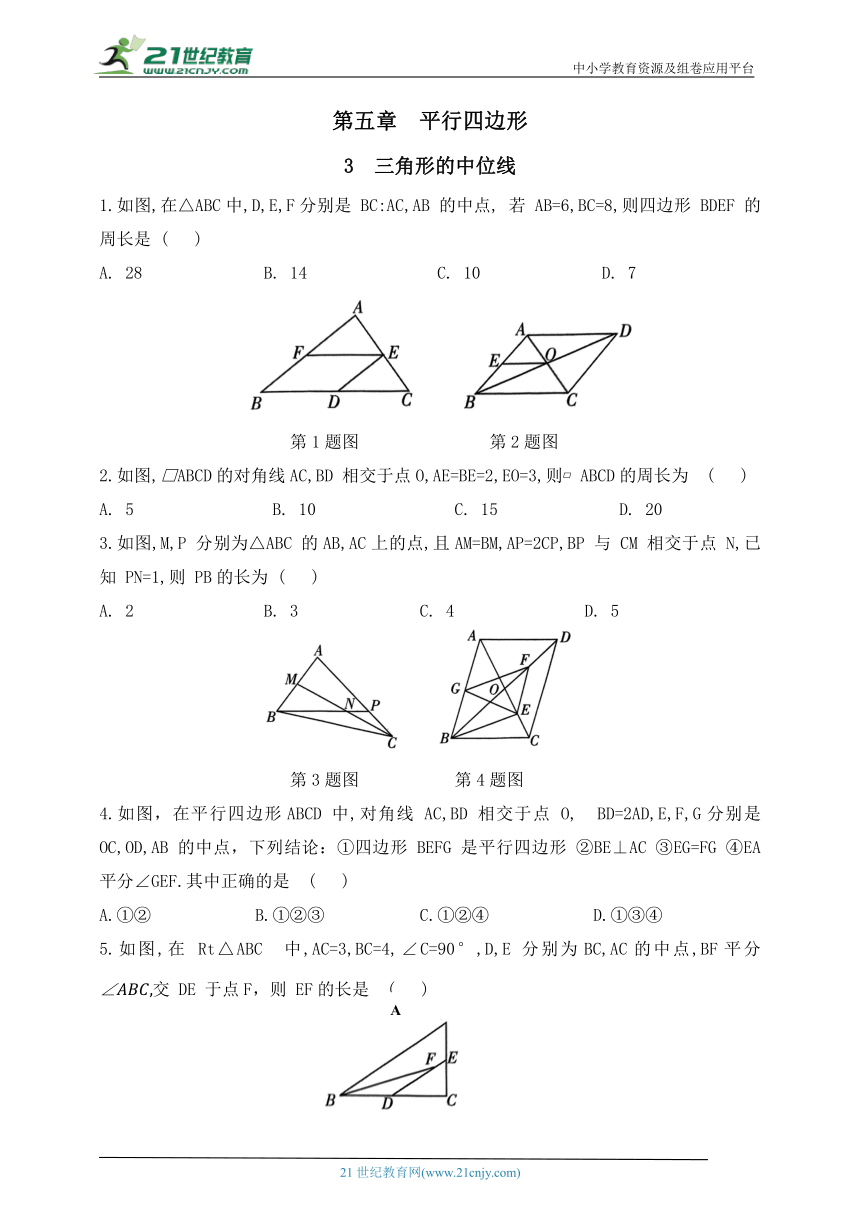
中小学教育资源及组卷应用平台 第五章 平行四边形 3 三角形的中位线 1.如图,在△ABC中,D,E,F分别是 BC:AC,AB 的中点, 若 AB=6,BC=8,则四边形 BDEF 的周长是 ( ) A. 28 B. 14 C. 10 D. 7 第1题图 第2题图 2.如图,□ABCD的对角线AC,BD 相交于点O,AE=BE=2,EO=3,则 ABCD的周长为 ( ) A. 5 B. 10 C. 15 D. 20 3.如图,M,P 分别为△ABC 的AB,AC上的点,且AM=BM,AP=2CP,BP 与 CM 相交于点 N,已知 PN=1,则 PB的长为 ( ) A. 2 B. 3 C. 4 D. 5 第3题图 第4题图 4.如图，在平行四边形ABCD 中,对角线 AC,BD 相交于点 O, BD=2AD,E,F,G分别是OC,OD,AB 的中点，下列结论：①四边形 BEFG 是平行四边形 ②BE⊥AC ③EG=FG ④EA平分∠GEF.其中正确的是 ( ) A.①② B.①②③ C.①②④ D.①③④ 5.如图,在 Rt△ABC 中,AC=3,BC=4,∠C=90°,D,E 分别为BC,AC的中点,BF平分 交 DE 于点F，则 EF的长是 ( ) B. 1 C. 2 6.如图, 的周长为8,对角线AC,BD 相交于点 M,延长AB到点E，使 于点N，连接MN,则MN=_____. 第6题图 第7题图 7.如图所示,在△ABC中,AB=13,BC=12,点 D,E 分别是AB,BC的中点,连接DE,CD,如果 DE=2.5,则△ACD 的周长为_____. 8.已知△ABC的周长为1，连接其三边中点构成第二个三角形，再连接第二个三角形三边的中点构成第三个三角形……以此类推，则第2025 个三角形的周长为_____. 第8题图 第9题图 9.如图, ABCD的顶点C 在等边△BEF 的边 BF 上,点 E 在 AB 的延长线上,G为DE 的中点,连接CG.若AD=3,AB=CF=2,则 CG的长为_____. 10.如图所示,在四边形ABCD 中, 点 M,N,E,F分别是BD,AC,BC,MN的中点,连接ME,NE. (1)试猜想 的形状，并证明你的猜想； (2)EF 与 MN 有何位置关系 请证明你的结论. 11.如图1,在平行四边形 ABCD中,点 E,F分别为AD，BC的中点，点 G，H 在对角线BD 上,且BG=DH. (1)求证：四边形 EHFG 是平行四边形； (2)如图 2,连接 AC,交 BD 于点 O,若求HF的长. 12.【三角形中位线定理】 已知：如图1，在 中,点 D,E分别是边AB，AC的中点.直接写出 DE 和 BC 的关系; 【应用】 如图2,在四边形 ABCD 中,点 E,F 分别是边AB,AD的中点,若. 2, 求 的度数； 【拓展】 如图3,在四边形 ABCD中,AC 与 BD 相交于点 E,点 M,N 分别为 AD,BC 的中点,MN 分别交AC,BD 于点 F,G, EG.求证: 参考答案 1. B 2. D 3. C 4. C 5. A 6. 2 7. 18 10.解:(1)△MEN 是等腰三角形.理由如下: ∵点 M,E是BD,BC的中点,∴ME 是 的中位线， 同理， 是等腰三角形； (2)EF⊥MN.理由如下: 由(1),得△MEN 是等腰三角形. ∵点 F 是 MN 的中点,∴EF⊥MN. 11.解:(1)证明:∵四边形 ABCD是平行四边形, ∴AD=BC,AD∥BC,∴∠EDH=∠FBG, ∵点 E,F分别为 ABCD的边AD,BC的中点,∴DE=BF, 在 与△BFG中, ∴EH∥FG, ∴四边形 EHFG是平行四边形； (2)∵四边形ABCD是平行四边形， ∴OA=OC=3,OB=OD, ∵BG=DH,∴BG-GH=DH-GH,即BH=DG, ∴OB-BH=OD-DG,即OH=OG, ∵HG=2BH,∴BH=OH, ∵点 F 为BC 的中点,∴HF 是△OBC的中位线, 12.解：【三角形中位线定理】 ∥ 【应用】连接BD,如图2, ∵E,F分别是边AB,AD的中点,∴EF∥BD,BD=2EF=4,∴∠ADB=∠AFE=45°, ∵BC=5,CD=3, ∴∠BDC=90°,∴∠ADC=∠ADB+∠BDC=135°; 【拓展】证明:取 DC 的中点 H,连接 MH,NH,如图3, ∵点 M,H分别是AD,DC的中点,∴MH是△ADC的中位线, ∴MH∥AC且 同理,得 NH∥BD且 ∵EF=EG,∴∠EFG=∠EGF, ∵MH∥AC,NH∥BD,∴∠EFG=∠HMN,∠EGF=∠HNM, ∴∠HMN=∠HNM,∴MH=NH, 21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页） 21世纪教育网(www.21cnjy.com) ... ...