第一章 特殊平行四边形专题训练（含答案）

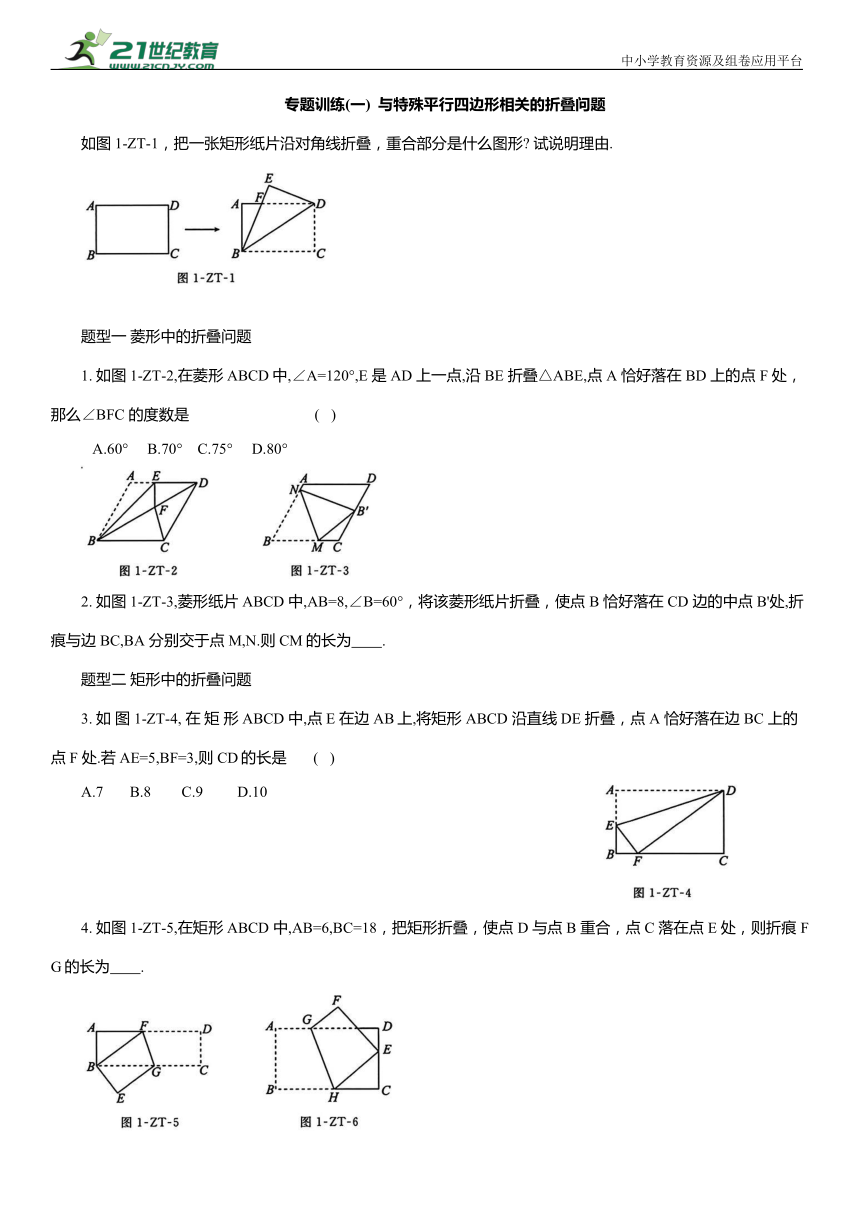
专题训练(一) 与特殊平行四边形相关的折叠问题 如图1-ZT-1，把一张矩形纸片沿对角线折叠，重合部分是什么图形 试说明理由. 题型一 菱形中的折叠问题 1. 如图1-ZT-2,在菱形 ABCD中,∠A=120°,E 是AD 上一点,沿 BE 折叠△ABE,点 A 恰好落在BD 上的点 F 处，那么∠BFC 的度数是 ( ) A.60° B.70° C.75° D.80° 2. 如图1-ZT-3,菱形纸片 ABCD 中,AB=8,∠B=60°，将该菱形纸片折叠，使点 B 恰好落在CD 边的中点B'处,折痕与边 BC,BA 分别交于点 M,N.则CM的长为 . 题型二 矩形中的折叠问题 3. 如 图 1-ZT-4, 在 矩 形ABCD 中,点 E 在边AB上,将矩形 ABCD 沿直线DE 折叠，点 A 恰好落在边 BC 上的点 F 处.若AE=5,BF=3,则CD的长是 ( ) A.7 B.8 C.9 D.10 4. 如图1-ZT-5,在矩形 ABCD 中,AB=6,BC=18，把矩形折叠，使点 D 与点 B 重合，点C 落在点E 处，则折痕 FG的长为 . 5. 如图1-ZT-6,折叠矩形纸片 AB-CD,使点B 的对应点 E 落在CD边上,GH 为折痕,已知AB=6,BC=10.当折痕GH 最长时,线段 BH 的长为 . 6. 如图 1-ZT-7,在矩形纸片 ABCD 中,已知AD=8,折叠纸片,使 AB 边落在对角线AC上,点 B 落在点 F 处,折痕为 AE,且 EF=3,求AB 的长. 7. 如图1-ZT-8,在矩形 ABCD中,点 E,F 分别在BC,AD 上,沿 EF 将矩形折叠,使点 C 与点A 重合，点D 落在点G 处. (1)求证:AE=AF; (2)若AB=4,BC=8,求△ABE的面积. 题型三 正方形中的折叠问题 8. 将正方形纸片按如图1-ZT-9 所示折叠，AM为折痕，点B落在对角线AC 上的点 E 处，则∠EMC 的度数为 ( ) A.22.5° B.30° C.45° D.67.5° 9. 如图1-ZT-10,将正方形 ABCD 沿BE 对折,使点 A 落在对角线 BD 上的点 处，连接 ,则∠BA'C= °. 10. 如图1-ZT-11,在边长为 12 的正方形 AB-CD 中,点 E 在边 BC 上, BE = 2CE,将△DCE 沿 DE 折叠至△DFE,延长 EF 交AB 于点G,连接 DG. (1)求∠GDE的度数; (2)求 AG的长度. 专题训练(二) 与正方形有关的常考模型 模型一 正方形中的“十字架”模型 方法点睛 正方形内，分别连接两组对边上任意两点，得到的两条线段(如图 2-ZT-1①中的线段 AF 与BE,图②中的线段AF与EG，图③中的线段 HF 与EG)满足：若两条线段垂直，则这两条线段相等. 1. 如图 2-ZT-2,正方形 ABCD 中,点 M,N分别在AB,BC上,且BM=CN,AN与 DM 相交于点 P. (1)求证:△ABN≌△DAM; (2)求∠APM的大小. 变式 如图2-ZT-3,在正方形ABCD 中,E,F 分别在CD,BC边上,AE 与 DF 相交于点P,∠APD=90°,那么AE 和DF的数量关系是 ；DE 和CF 的数量关系是 . 模型二 正方形中过对角线交点的直角模型 方法点睛 如图2-ZT-4，在正方形ABCD中，O为对角线的交点,直角∠EOF 绕点O 顺时针旋转,若OE,OF 分别与DA,AB的延长线交于点 G,H,则△AGO≌△BHO,△OGH是等腰直角三角形. 2. 如图2-ZT-5,正方形 ABCD中,O为对角线AC 的中点,P 为平面内一点,且 BP⊥CP.过点O作OE⊥OP 交 PB 的延长线于点 E. (1)探究 BE 与 PC 之间的数量关系，并说明理由； (2)直接写出 BP,CP,OP 三者之间存在的关系. 变式 如图2-ZT-6,在等腰直角三角形 ABC中,∠C=90°,O是 AB 的中点,且 AC=1，将一块三角尺的直角顶点放在点O处，始终保持该三角尺的两直角边分别与 AC，BC相交，交点分别为 D，E，则这两个三角形重叠部分的面积为 . 模型三 外角平分线模型 方法点睛 在正方形 ABCD中，点E在射线CB 上，EF交外角∠DCG的平分线(图2-ZT-7①)或其所在直线(图②)于点 F,AE⊥EF,则有AE=EF. 3. 如图2-ZT-8,四边形 ABCD 是正方形,E 是边BC 上任意一点,∠AEF=90°,且 EF 交正方形外角的平分线CF 于点 F. 求证:AE=EF. 变式 如图2-ZT-9,四边形 ABCD 是正方形,E 是边BC 上一点,且∠AEF=90°，EF 交正方形外角平分线CF 于点 F.若正方形的边长是8,EC=2,则FC的长为 . 模型四 半角模型 方法点睛 如图2-ZT- ... ...