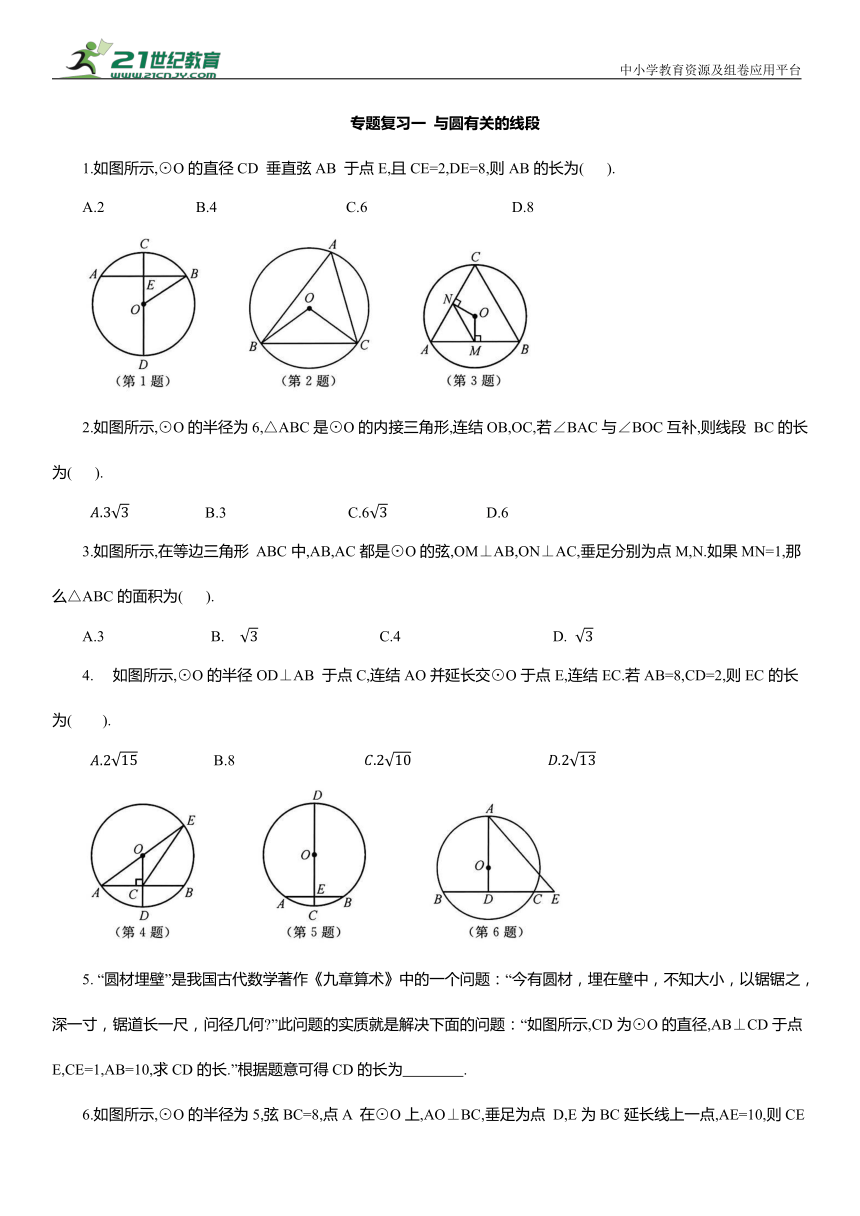
中小学教育资源及组卷应用平台 专题复习一 与圆有关的线段 1.如图所示,⊙O的直径CD 垂直弦AB 于点E,且CE=2,DE=8,则AB的长为( ). A.2 B.4 C.6 D.8 2.如图所示,⊙O的半径为6,△ABC是⊙O的内接三角形,连结OB,OC,若∠BAC与∠BOC互补,则线段 BC的长为( ). B.3 C.6 D.6 3.如图所示,在等边三角形 ABC中,AB,AC都是⊙O的弦,OM⊥AB,ON⊥AC,垂足分别为点M,N.如果MN=1,那么△ABC的面积为( ). A.3 B. C.4 D. 如图所示,⊙O的半径OD⊥AB 于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长 为( ). B.8 5. “圆材埋壁”是我国古代数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何 ”此问题的实质就是解决下面的问题:“如图所示,CD为⊙O的直径,AB⊥CD于点E,CE=1,AB=10,求CD的长.”根据题意可得CD的长为 . 6.如图所示,⊙O的半径为5,弦BC=8,点A 在⊙O上,AO⊥BC,垂足为点 D,E为BC延长线上一点,AE=10,则CE的长为 . 7.如图所示,AB是半圆O的直径,BC是弦,点 P 从点A 开始,沿AB 向点B 以1cm/s的速度移动,若AB为10cm,点O到BC 的距离为4cm. (1)求弦BC的长. (2)经过几秒,△BPC是等腰三角形 8.如图所示,△ABC是⊙O的内接等边三角形,弦EF 经过BC 的中点D,且EF∥BA,若⊙O的半径为 ,则DE的长为( ). 9.如图所示,AB是⊙O的直径,AB=2,OC是⊙O的半径,OC⊥AB,点 D在. 上, ,P 是半径OC 上一个动点,那么AP+PD的最小值为 . 10.如图所示,⊙O的直径AB=10,P 是OA 上一点,弦 MN 过点 P,且AP=2,MP=2,弦心距OQ为 . 11.小明学习了垂径定理后,做了以下探究,请根据题目要求帮小明完成探究. (1)更换定理的题设和结论可以得到许多真命题.如图1所示,在⊙O中,C是劣弧AB的中点,直线CD⊥AB 于点E,则AE=BE.请证明此结论. (2)从圆上任意一点出发的两条弦所组成的折线,称为该圆的一条折弦.如图2所示,PA,PB组成⊙O的一条折弦,C是劣弧AB 的中点,直线CD⊥PA于点 E,则AE=PE+PB.可以通过延长DB,AP 相交于点 F,再连结AD证明结论成立.请写出证明过程. (3)如图3所示,PA,PB组成⊙O的一条折弦,若C是 的中点,直线CD⊥PA于点E,则AE,PE与PB之间存在怎样的数量关系 写出结论,不必证明. 12.如图所示,在半径为3的⊙O中,AB 是直径,AC 是弦,D 是的中点,AC与BD 交于点E.若E是BD 的中点,则AC的长为( ). 13.如图所示,△ABC内接于⊙O,∠ACB=90°,∠ACB 的平分线交⊙O于点D.若AC=6,BD=5,则BC的长为 . 14.要在半径为1、圆心角为60°的扇形 AOB 铁皮上截取一块尽可能大的正方形.小明设计如下两种截取方案. 方案一(如图1所示):点C在OA 上,点 D,E在OB 上,点 F在上. 方案二(如图2所示):点C在OA 上,点 D 在OB 上,点 E,F在 上. 请计算这两种方案中正方形铁皮的面积,帮小明选择合理的方案(参考数据: 专题复习一 与圆有关的线段 1. D 2. C 3. B 4. D 5.26 6.2 7.(1)如答图1所示,作OD⊥BC于点D, ∴BD=3(cm).∴BC=2BD=6(cm). (2)设经过t(s)后,△BPC是等腰三角形. ①当PC为底边时,BP=BC,10-t=6,解得t=4(s). ③当 PB为底边时,PC=BC.如答图2所示,连结AC,作CE⊥AB于点E,则 ∵AB是直径,∴△ABC是直角三角形. 解得t=2.8(s). 综上可知,经过4s或5s或2.8s后,△BPC 是等腰三角形. 8. C 9. 10. 11.(1)如答图所示,连结AD,BD. ∵C是劣弧AB 的中点, ∴∠CDA=∠CDB. ∴△ADB为等腰三角形. ∵CD⊥AB,∴AE=BE. (2)∵四边形 ADBP 是圆内接四边形,∴∠PBD+∠PAD=180°. ∵∠PBD+∠PBF=180°,∴∠PBF=∠PAD. ∵C是劣弧AB 的中点,∴∠CDA=∠CDF. ∵CD⊥PA,∴△AFD为等腰三角形. ∴∠F=∠A,AE=EF. ∴∠PBF=∠F.∴PB=PF. ∴AE=PE+PB. (3)AE=PE-PB. 12. D 【解析】连结OD交AC 于点 F. ∵D是AC的中点,∴OD⊥AC,AF=CF. ∴∠DFE=90°. ∵OA=OB,AF=CF,∴OF= BC ... ...
~~ 您好,已阅读到文档的结尾了 ~~

