18.1勾股定理 同步练习（含答案）

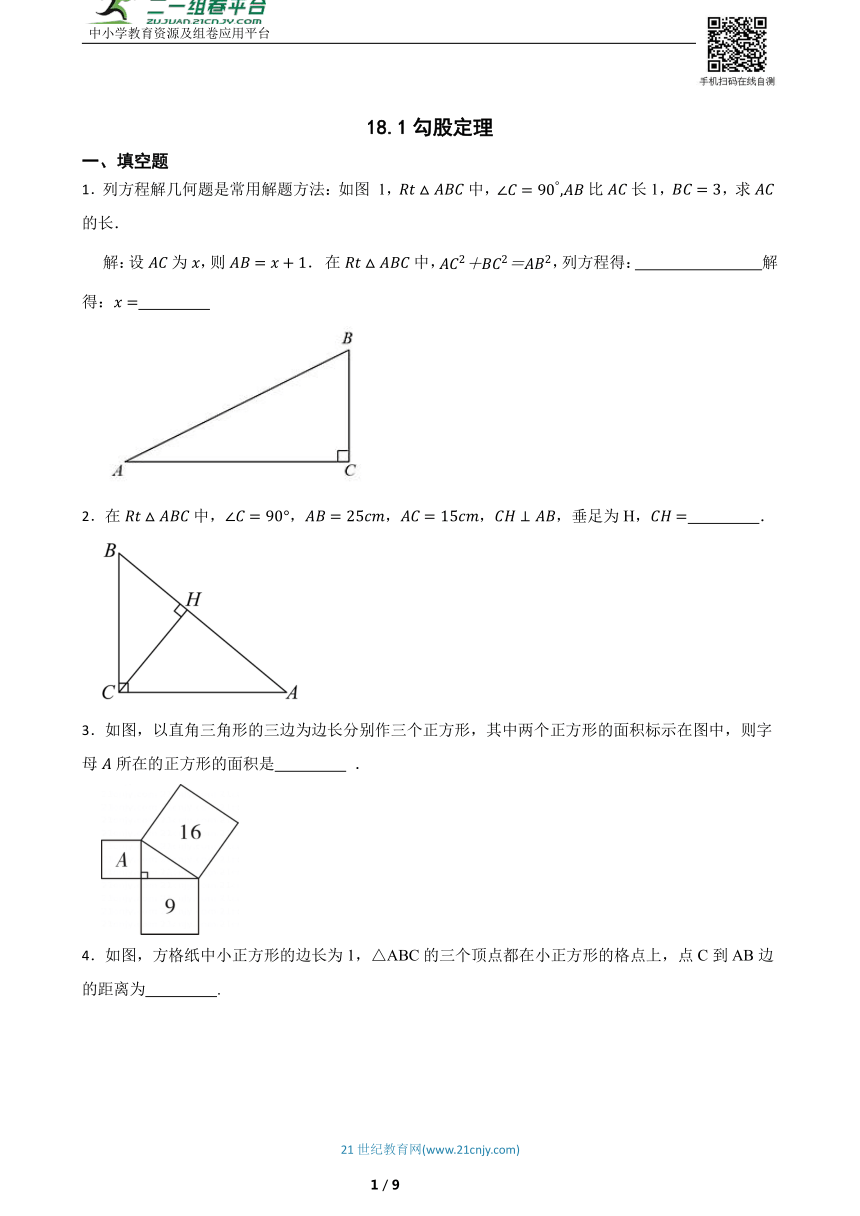
中小学教育资源及组卷应用平台 18.1勾股定理 一、填空题 1．列方程解几何题是常用解题方法：如图 1，中，比长1，，求的长． 解：设为，则． 在中，，列方程得：　 　解得：　 　 2．在中，，，，，垂足为H，　 　． 3．如图，以直角三角形的三边为边长分别作三个正方形，其中两个正方形的面积标示在图中，则字母所在的正方形的面积是　 　 ． 4．如图，方格纸中小正方形的边长为1，△ABC的三个顶点都在小正方形的格点上，点C到AB边的距离为　 　. 5．如图，在△ABC中，AB＝AC＝13，BC＝10，D为BC上一点，若BD＝5，则AD的长为　 　. 6．在平面直角坐标系中，点的坐标为，则点到坐标原点的距离为　 　． 二、单选题 7．在中，所对边分别为，若，则面积为（　　） A． B． C．3 D． 8．已知直角三角形的一条边长为10，另一边长为8，则第三边长为（　　） A．6 B．8 C． D．6或 9．如图，图1是第七届国际数学教育大会（）会徽，在其主体图案中选择两个相邻的直角三角形，恰好能组合得到如图2所示的四边形．若，，则的值为（　　） 图1 图2 A．6 B．5 C．4 D．3 10．已知直角三角形的两边长是3，5，那么斜边可能是（　　） A．3 B．4 C．5 D．6 11．我国古代数学家刘徽将勾股形（古人称直角三角形为勾股形）分割成一个正方形和两对全等的直角三角形，得到一个恒等式，后人借助此分割方法所得图形证明了勾股定理．如图所示，矩形就是由两个这样的图形拼成（无重叠、无缝隙）．下面给出的条件中，一定能求出矩形面积的是（　　） A．与的积 B．与的积 C．与的积 D．与的积 三、解答题 12．如图，学校要测量旗杆的高度，同学们发现系在旗杆顶端的绳子垂到地面并多出一段（如图1），同学们首先测量了多出的这段绳子长度为1米，再将绳子拉直（如图2），测出绳子末端到旗杆底部的距离为5米，求旗杆的高度． 四、计算题 13．在苏教版七下第九章的学习中，对同一个图形的面积可以从不同的角度思考，用不同的式子表示． （1）用不同的方法计算图1的面积得到等式：_____． （2）图2是由两个边长分别为a、b、c的直角三角形和一个两条直角边都是c的直角三角形拼成，从整体看它又是一个直角梯形，用不同的方法计算这个图形的面积，能得到等式：_____（结果为最简） （3）根据上面两个结论，解决下面问题： ①在直角中，，三边长分别为a、b、c，已知，，求的值． ②如图3，四边形中，对角线，互相垂直，垂足为O，，在直角中，，，若的周长为2，则的面积=_____． 14．如图，在平面直角坐标系中，点是坐标原点，点，点，其中满足； （1）求的值； （2）点从点出发，以每秒2个单位长度的速度沿轴正半轴运动，连接，设点的运动时间为秒，的面积为，用含的式子表示，并直接写出相应的取值范围； （3）在（2）的条件下，点在上，点在延长线上，，当时，求点的坐标． 15．如图，C为线段上一动点，分别过点B，D作，连接．已知． （1）求当x等于何值时， （2）当时，求的长． （3）利用图形求代数式的最小值． 五、作图题 16．在如图所示的 方格中， 每个小方格的边长都为 1 ． （1）在图中画出长度为 与 的线段，要求线段的端点在格点上； （2） 在图中画出一个三条边长分别为 3 ， 的三角形， 使它的顶点都在格点上． 六、综合题 17．川藏铁路是一条连接四川省与西藏自治区的快速铁路，是我国铁路建设工程的里程碑，在建设过程中，某工程队准备从A到B修建一条隧道，测量员在的同一侧选定C，D两个观测点，如图，测得长为，长为，长为，，．（A，B，C，D在同一水平面内）． （1）求A，D两点之间的距离． （2）求隧道的长度． 18．在Rt△ABC中，∠C=90° （1）已知a=6， c=10，求b， （2）已知a=40，b=9，求c； （3）已知c=25，b=15，求a. 19．为了把家乡建 ... ...