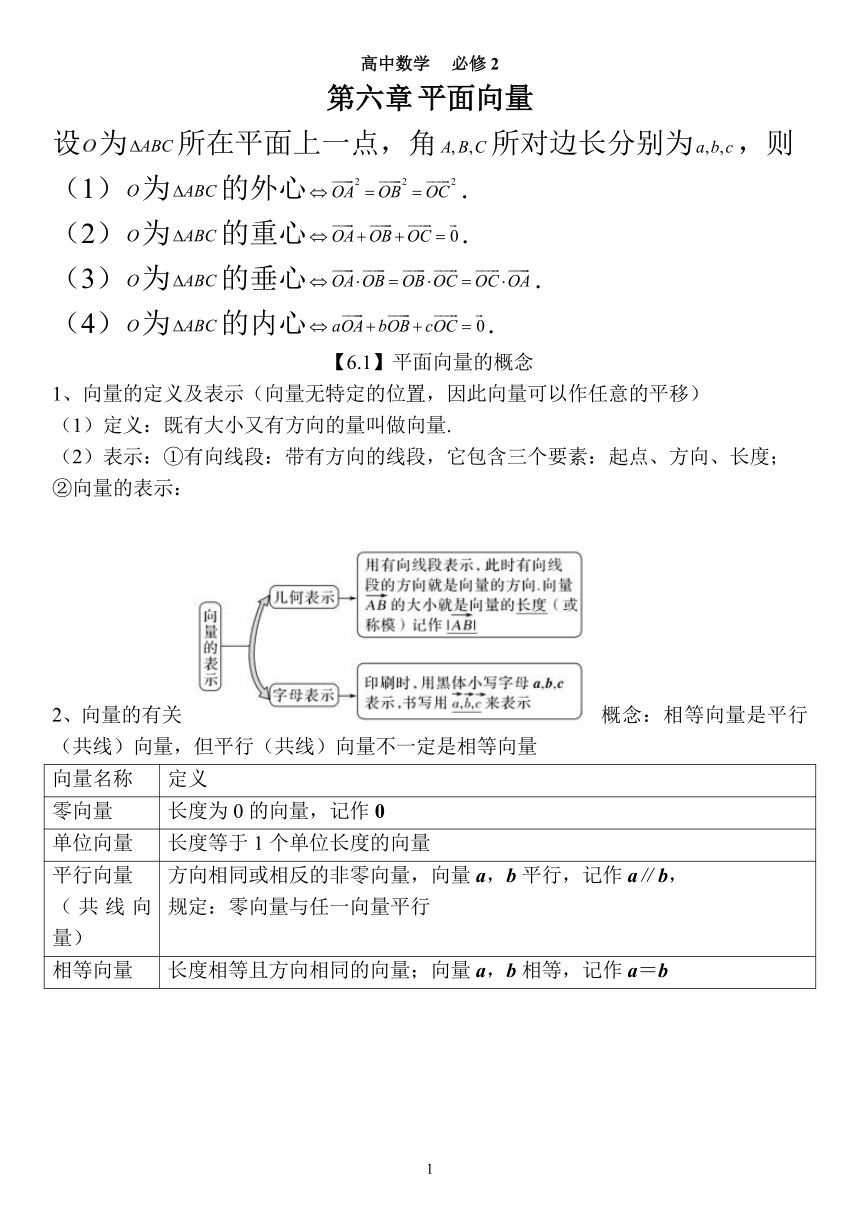
高中数学 必修 2 第六章平面向量 设 为 ABC所在平面上一点,角 A,B,C所对边长分别为 a,b,c,则 (1)O为 的外心 2 2 2 ABC OA OB OC . 2 ( )O为 ABC的重心 OA OB OC 0 . 3 ( )O为 ABC的垂心 OA OB OB OC OC OA . 4 ( )O为 ABC的内心 aOA bOB cOC 0 . 【6.1】平面向量的概念 1、向量的定义及表示(向量无特定的位置,因此向量可以作任意的平移) (1)定义:既有大小又有方向的量叫做向量. (2)表示:①有向线段:带有方向的线段,它包含三个要素:起点、方向、长度; ②向量的表示: 2、向量的有关 概念:相等向量是平行 (共线)向量,但平行(共线)向量不一定是相等向量 向量名称 定义 零向量 长度为 0的向量,记作 0 单位向量 长度等于 1个单位长度的向量 平行向量 方向相同或相反的非零向量,向量 a,b 平行,记作 a∥b, ( 共 线 向 规定:零向量与任一向量平行 量) 相等向量 长度相等且方向相同的向量;向量 a,b 相等,记作 a=b 1 【6.2】平面向量的运算 1、向量的加法 (1)定义:求两个向量和的运算. (2)运算法则: 向量求和的法则 图示 几何意义 三角形法则 已知非零向量 a,b,在平面内任取一 使用三角形法则时要注意 点 A,作� �� ��=a, ��� ��=b,则向量 ��� � “首尾相接”的条件,而向量 叫做 a 与 b 的和,记作 a+b,即 a+b 加法的平行四边法则应用的 = ��� ��+� �� ��=� �� � 前提是共起点 平行四边形法则 以同一点 O 为起点的两个已知向量 a,b,以 OA,OB为邻边作 OACB, 则以 O 为起点的向量 ��� ��(OC 是 OACB的对角线)就是向量 a 与 b 的和 (3)规定:对于零向量与任意向量 a,规定 a+0=0+a=a. (4)位移的合成可以看作向量加法三角形法则的物理模型;力的合成可以看作向量加 法平行四边形法则的物理模型. (5)一般地我们有|a+b|≤|a|+|b|,当且仅当 a,b 方向相同时等号成立. (6)向量加法的运算律与实数加法的运算律相同 2、向量的减法 (1)相反向量(利用相反向量的定义,- ��� ��=� �� ��就可以把减法转化为加法) 定义:我们规定,与向量 a 长度相等,方向相反的向量,叫做 a 的相反向量 性质:①对于相反向量有:a+(-a)=0;②若 a,b 互为相反向量,则 a=-b,a +b=0;③零向量的相反向量仍是零向量 (2)向量减法运算(向量的减法是向量加法的一种逆运算) 定义:求两个向量差的运算叫做向量的减法. a-b=a+(-b),减去一个向量就等于加上这个向量的相反向量. 几何意义:a-b 表示为从向量 b 的终点指向向量 a 的终点的向量. 3、向量的数乘运算(实数与向量可以进行数乘运算,但不能进行加减运算) (1)定义:规定实数λ与向量 a 的积是一个向量,这种运算叫做向量的数乘,记作:λa, 它的长度和方向规定如下: ①|λa|=|λ||a|;②当λ>0时,λa 的方向与 a 的方向相同;当λ<0时,λa 的方向与 a 的方 向相反. ③由①可知,当λ=0时,λa=0;由①②知,(-1)a=-a. 2 (2)运算律:设λ,μ为任意实数,则有:①λ(μa)=(λμ)a;②(λ+μ)a=λa+μa; ③λ(a+b)=λa+λb; 特别地,有(-λ)a=-(λa)=λ(-a);λ(a-b)=λa-λb. (3)向量的加、减、数乘运算统称为向量的线性运算,向量的线性运算结果仍是向 量.对于任意向量 a,b,以及任意实数λ,μ1,μ2,恒有λ(μ1 a±μ2b)=λμ1 a±λμ2 b. (4)共线向量定理:向量 a(a≠0)与 b 共线的充要条件是:存在唯一一个实数λ,使 b=λa.也就是说,位于同一直线上的向量可以由位于这条直线上的一个非零向量表示. 4、向量的数量积 (1)向量的夹角:两向量的夹角与两直线的夹角的范围不同,向量夹角范围是[0,π], 而两直线夹角的范围为 0, 2 (2)向量的夹角的定义:已知两个非零向量 a, ... ...
~~ 您好,已阅读到文档的结尾了 ~~