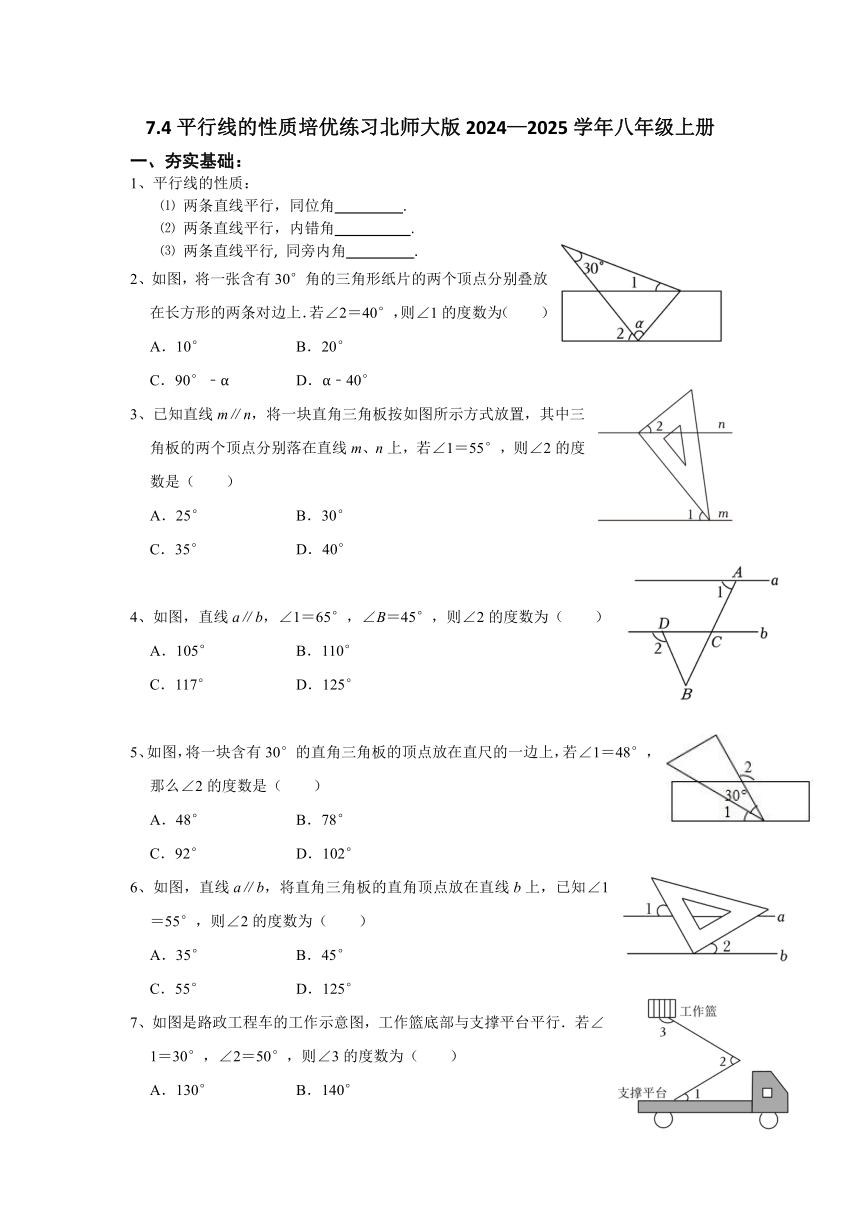
7.4平行线的性质培优练习北师大版2024—2025学年八年级上册 夯实基础: 1、平行线的性质: ⑴ 两条直线平行,同位角 . ⑵ 两条直线平行,内错角 . ⑶ 两条直线平行, 同旁内角 . 2、如图,将一张含有30°角的三角形纸片的两个顶点分别叠放在长方形的两条对边上.若∠2=40°,则∠1的度数为( ) A.10° B.20° C.90°﹣α D.α﹣40° 3、已知直线m∥n,将一块直角三角板按如图所示方式放置,其中三角板的两个顶点分别落在直线m、n上,若∠1=55°,则∠2的度数是( ) A.25° B.30° C.35° D.40° 4、如图,直线a∥b,∠1=65°,∠B=45°,则∠2的度数为( ) A.105° B.110° C.117° D.125° 5、如图,将一块含有30°的直角三角板的顶点放在直尺的一边上,若∠1=48°,那么∠2的度数是( ) A.48° B.78° C.92° D.102° 6、如图,直线a∥b,将直角三角板的直角顶点放在直线b上,已知∠1=55°,则∠2的度数为( ) A.35° B.45° C.55° D.125° 7、如图是路政工程车的工作示意图,工作篮底部与支撑平台平行.若∠1=30°,∠2=50°,则∠3的度数为( ) A.130° B.140° C.150° D.160° 8、如图,将正方形纸片ABCD折叠,使点D落在边AB上的点D′处,点C落在点C′处,若∠AD′M=60°,则∠MNB的度数为( ) A.65° B.70° C.75° D.80° 一张长方形纸片按如图所示方式折叠后,若∠1=50°, 则∠2= . 10、如图,把一张长方形的纸按图那样折叠后,B,D两点落在B′,D′点处,若∠AOB′=76°,则∠CGO的度数是 . 11、如图,已知AD∥BC,点E,F在AD边上,点G,H在BC边上,分别沿EG,FH折叠,使点D和点A都落在点M处,若α=60°,β=50°,则∠FEM的度数为 ,∠EMF的度数为 . 二、例题精讲: 例1、如图,EF⊥BC,∠1=∠C,∠2+∠3=180°,试说明∠ADC=90°.请完善解答过程,并在括号内填写相应的理论依据. 解:∵∠1=∠C,(已知) ∴GD∥ .( ) ∴∠2=∠DAC.( ) ∵∠2+∠3=180°,(已知) ∴∠DAC+∠3=180°.(等量代换) ∴AD∥EF.( ) ∴∠ADC= .(两直线平行,同位角相等) ∵EF⊥BC,(已知) ∴∠EFC=90°.( ) ∴∠ADC=90°.(等量代换) 变式1、完成下面的解题过程,并在括号内填上依据: 如图,已知AB∥CD,∠1=∠2,∠3=∠4,试说明AD∥BE. 解:∵AB∥CD(已知), ∴∠4=∠ ( ), ∵∠3=∠4(已知), ∴∠3=∠ ( ), ∵∠1=∠2(已知), ∴∠1+∠CAF=∠2+∠CAF, 即∠BAE=∠DAC, ∴∠3=∠ , ∴AD∥BE( ). 例2、如图,D、E、F、G是△ABC边上的点,DE∥AC,∠ADE=∠CGF. (1)试证:AD∥GF; (2)若AD平分∠BAC,∠AED=100°,∠C=56°,求∠CFG的度数. 变式1、已知:如图所示,AB∥CD,EF平分∠GFD,GF交AB于M,∠GMA=52°,求∠BEF的度数. 变式2、如图,在△ABC中,∠A=70°,∠B=50°,CD是∠ACB的平分线,DE∥BC,交AC于点E. (1)求∠CDE的度数. (2)若点F为CD中点,连结EF.求证:EF⊥CD. 变式3、如图,在三角形ABC中,点E、点G分别是边AB、AC上的点,点F、点D是边BC上的点,连接EF、AD和DG,DG是∠ADC的角平分线,若∠1+∠2=180°,AB∥DG,∠2=145°,求∠EFC的度数. 变式4、如图,BE是△ABC的角平分线,过E作EF∥AB交△ABC的外角∠CBD的平分线于点F,交边BC于点G. (1)∠EBF的大小为 度; (2)求证:G为线段EF的中点. 例3、如图,AE⊥BC,FG⊥BC,垂足分别是M、N,且∠1=∠2. (1)求证:AB∥CD; (2)若∠CBD=70°,∠D﹣∠3=56°,求∠C的度数. 变式1、如图,∠B=∠CDF,∠ ... ...
~~ 您好,已阅读到文档的结尾了 ~~