11.2图形的旋转 同步练习 （无答案）青岛八年级下册数学

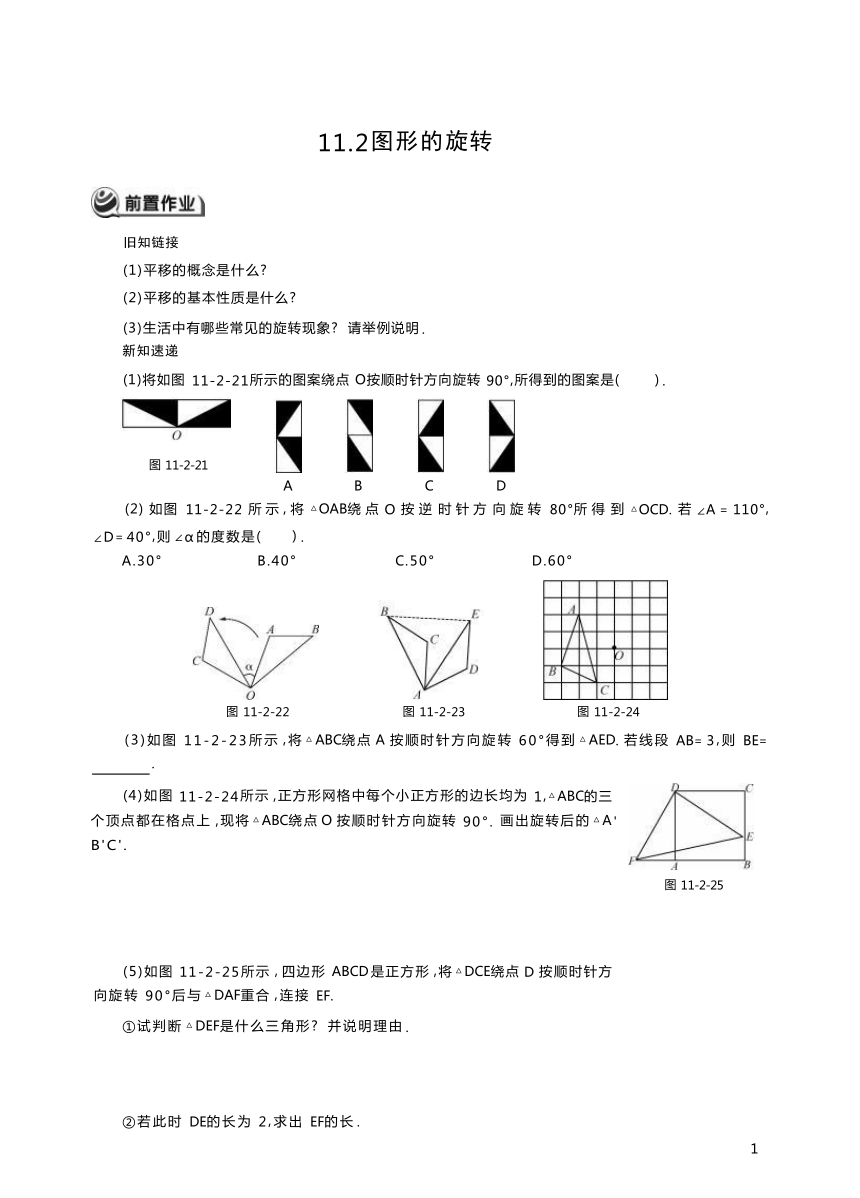
11.2图形的旋转 旧知链接 (1)平移的概念是什么 (2)平移的基本性质是什么 (3)生活中有哪些常见的旋转现象 请举例说明 . 新知速递 (1)将如图 11-2-21所示的图案绕点 O按顺时针方向旋转 90°,所得到的图案是( ) . 图 11-2-21 A B C D (2) 如图 11-2-22 所 示 , 将 △OAB绕 点 O 按 逆 时 针 方 向 旋 转 80°所 得 到 △OCD. 若 ∠A = 110°, ∠D= 40°,则 ∠α 的度数是( ) . A.30° B.40° C.50° D.60° 图 11-2-22 图 11-2-23 图 11-2-24 (3)如图 11-2-23所示 ,将 △ABC绕点 A 按顺时针方向旋转 60°得到 △AED. 若线段 AB= 3,则 BE= 1 . (4)如图 11-2-24所示 ,正方形网格中每个小正方形的边长均为 1,△ABC的三 个顶点都在格点上 ,现将 △ABC绕点 O 按顺时针方向旋转 90°. 画出旋转后的 △A' B'C'. (5)如图 11-2-25所示 , 四边形 ABCD 是正方形 ,将 △DCE绕点 D 按顺时针方 向旋转 90°后与 △DAF重合 ,连接 EF. ①试判断 △DEF是什么三角形 并说明理由 . ②若此时 DE的长为 2,求出 EF的长 . 图 11-2-25 (1)将如图 11-2-27所示的大写字母 E绕点 P 按顺时针方向旋转 90°得到的图形是( ) . 图 11-2-27 A B C D (2)如图 11-2-28所示 ,将 △ABC绕点 C 按顺时针方向旋转至 △A'B'C 的位置 . 若 ∠ACB= 15°, ∠B= 120°,则 ∠A'的度数为 . 图 11-2-28 图 11-2-29 图 11-2-30 (3)如图 11-2-29所示 ,在 △ABC中 , ∠BAC= 90°,AB=AC,将 △AEC按顺时针方向转动一定角度后 得到 △AFB. ①图中哪一点是旋转中心 ②旋转了多少度 ③指出图中的对应点 、对应线段和对应角 . (4)如图 11-2-30所示 ,画出将 △ABC绕点 M 按顺时针方向旋转 60°后得到的图形 . (5)在 △ABC中 , ∠ACB= 90°,AC=BC,直线 MN 经过点 C,且 AD⊥MN 于点 D ,BE⊥MN 于点 E. ①当直线 MN 绕点 C 旋转到图 11-2-31①的位置时 ,写出 DE,AD,BE具有的数量关系 ,并说明理由 . ②当直线 MN 绕 点 C 旋 转 到 图 11-2-31②的 位 置 时 , 写 出 DE,AD, BE具 有 的 数 量 关 系 , 不 必 说 明 理由 . ③当直线 MN 绕点 C 旋 转 到 图 11-2-31③的 位 置 时 , DE,AD, BE具 有 怎 样 的 数 量 关 系 不 必 说 明 理由 . 图 11-2-31 基础训练 (1)下列 4 张牌中 ,若将其中 1 张牌旋转 180°后花色仍是它本身 ,则旋转的牌是( ) . A B C D (2)一个图形经过旋转变化 ,发生改变的是( ) . A. 旋转中心 B. 旋转角度 C. 图形的形状 D. 图形的位置 (3)如图 11-2-33所示 ,将四边形 OACB 绕点 O 按顺时针方向旋转到四边形 DOEF 的位置 ,在这个旋 转过程中 ,旋转中心是 ,旋转角是 ,AO 与 DO 的关系是 , ∠AOD与 ∠BOE 的关 系是 . 图 11-2-33 图 11-2-34 图 11-2-35 (4)如图 11-2-34所示 ,将 △OAB绕点 O 按逆时针方向旋转 30°至 △OA'B'的位置 ,使点 B恰好落在边 A'B'上 ,则 ∠ABO= °. 拓展提高 (1)如图 11-2-35所示 ,在 △ABC中 , ∠B= 40°. 将 △ABC绕点 A 按逆时针方向旋转至 △ADE的位置 , 使点 B落在 BC 延长线上的点 D 处 , ∠BDA= 40°,则 ∠BDE= . (2)如图 11-2-36所示 ,将字母 N 绕它右下侧的顶点按顺时针方向旋转 90°,画出旋转后的图形 . 图 11-2-36 图 11-2-37 (3)如图 11-2-37所示 , 将 一 个 钝 角 △ABC(其 中 ∠ABC= 120°) 绕 点 B 按 顺 时 针 方 向 旋 转 得 到 △A1 BC1 ,使得点C落在 AB的延长线上的点 C1处 ,连接 AA1 . ①写出旋转角的度数 . ②求证 : ∠A1AC= ∠C1 . 发散思维 (1)如图 11-2-38①所示 ,若四 边 形 ABCD 和 四 边 形 GFED 都 是 正 方 形 , 显 然 图 中 有 AG= CE,AG⊥ CE. 当正方形 GFED 绕点 D 旋转到如图 11-2-38②所示的位置时 ,AG=CE 是否成立 若成立 ,请给出证 明 ;若不成立 ,请说明理由 . 图 11-2-38 图 11-2-39 (2)如图 11-2-39所示 ,一副三 ... ...