6.3反比例函数的应用培优练习浙教版2024—2025学年八年级下册（含解析）

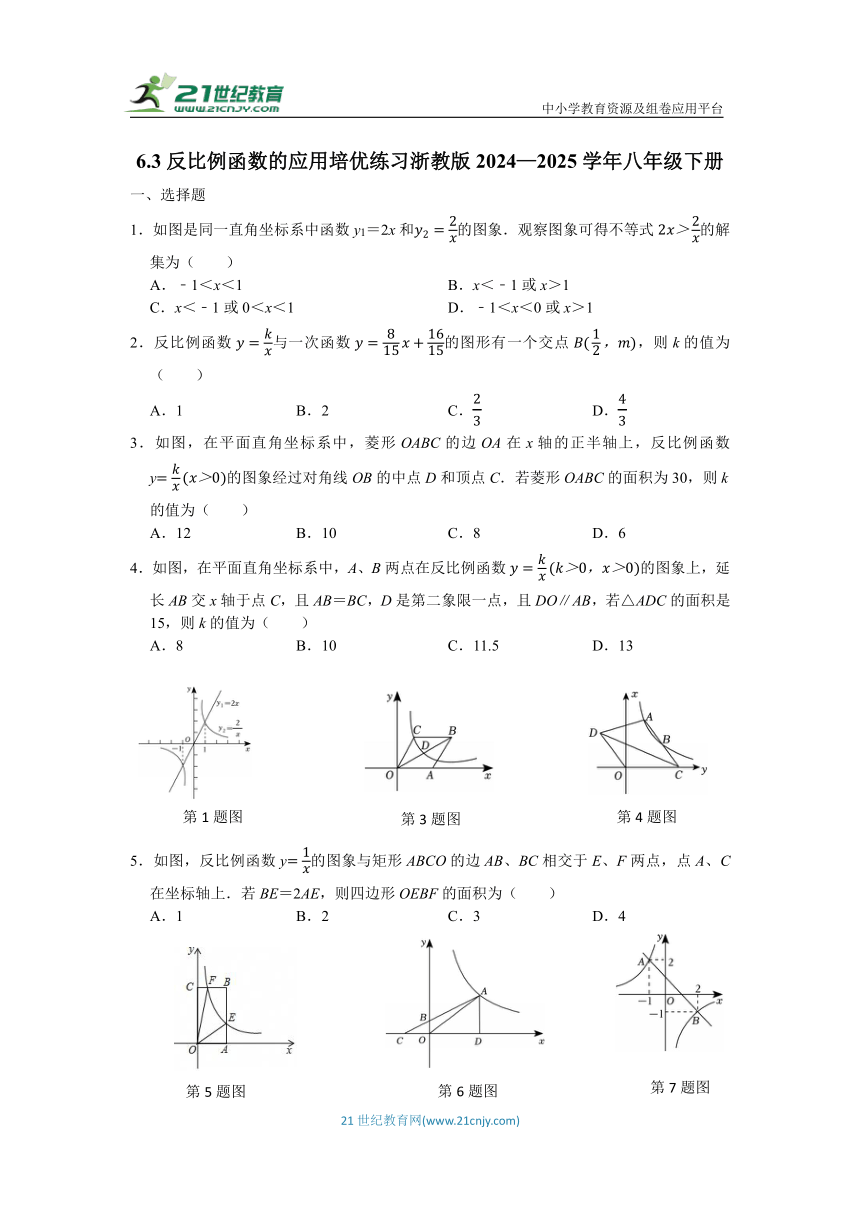
中小学教育资源及组卷应用平台 6.3反比例函数的应用培优练习浙教版2024—2025学年八年级下册 一、选择题 1．如图是同一直角坐标系中函数y1＝2x和的图象．观察图象可得不等式的解集为（　　） A．﹣1＜x＜1 B．x＜﹣1或x＞1 C．x＜﹣1或0＜x＜1 D．﹣1＜x＜0或x＞1 2．反比例函数与一次函数的图形有一个交点，则k的值为（　　） A．1 B．2 C． D． 3．如图，在平面直角坐标系中，菱形OABC的边OA在x轴的正半轴上，反比例函数y的图象经过对角线OB的中点D和顶点C．若菱形OABC的面积为30，则k的值为（　　） A．12 B．10 C．8 D．6 4．如图，在平面直角坐标系中，A、B两点在反比例函数的图象上，延长AB交x轴于点C，且AB＝BC，D是第二象限一点，且DO∥AB，若△ADC的面积是15，则k的值为（　　） A．8 B．10 C．11.5 D．13 5．如图，反比例函数y的图象与矩形ABCO的边AB、BC相交于E、F两点，点A、C在坐标轴上．若BE＝2AE，则四边形OEBF的面积为（　　） A．1 B．2 C．3 D．4 二、填空题 6．如图，点A是反比例函数图象上的一点，过点A作AD⊥x轴于点D，点C为x轴负半轴上一点且满足OD＝2OC，连接AC交y轴于点B，连接AO，若S△BOA＝3，则k的值为　 　． 7．如图，一次函数y1＝kx+b（k≠0）的图象与反比例函数为常数且m≠0）图象的都经过A（﹣1，2），B（2，﹣1），结合图象，则不等式的解集是　 　． 8．如图，点A，B是函数图象上两点，过点A作AC⊥x轴，垂足为点C，AC交OB于点D．若△ADO的面积为3，点D为OB的中点，则k的值为 　 　． 9．在平面直角坐标系中，直线y＝x﹣3与双曲线的图象交于点P（a，b），则代数式的值为 　 　． 10．已知双曲线y与函数y＝|x﹣a|的图象有两个交点，则a的值是 　 　． 三、解答题 11．如图，一次函数y1＝k1x+2（k1≠0）与反比例函数的图象交于点A（4，m）和B（﹣8，﹣2），与y轴交于点C． （1）求m，k1，k2的值； （2）点E（x1，yE），F（x2，yF），G（x3，yG）都在反比例函数的图象上，若x1＜x2＜0＜x3，比较yE，yF，yG的大小（用＜号连接），其结果是 　 　； （3）过点A作AD⊥x轴于点D，求△ABD的面积． 12．如图，一次函数y1＝x+6的图象与反比例函数（k为常数且k≠0）的图象交于A（﹣2，b），B两点． （1）求反比例函数的解析式； （2）连接OA，OB，求△AOB的面积． 13．如图，在平面直角坐标系中，点A（﹣3，0），B（0，﹣4），把线段AB绕点A逆时针旋转90°到AC，AC交y轴于点D，反比例函数（x＞0）的图象经过点C． （1）求k的值； （2）连接BC，若点P在反比例函数y（x＞0）的图象上，且S△BDP＝S△ABC，求点P的坐标． 14．如图，在平面直角坐标系中，直线l1：y＝k1x+b与反比例函数的图象交于A，B两点（点A在点B右侧），已知点A的坐标是（6，2），点B的纵坐标是﹣3． （1）求反比例函数和直线l1的表达式； （2）根据图象直接写出的解集； （3）将直线l1：y＝k1x+b沿y轴向上平移后的直线l2与反比例函数在第一象限内交于点C，如果△ABC的面积为15，求平移后的直线l2的函数表达式． 15．某水果生产基地在气温较低时，用装有恒温系统的大棚栽培一种新品种水果，如图是试验阶段的某天恒温系统从开启到关闭后，大棚内的温度y（℃）与时间x（h）之间的函数关系，其中线段OB、BC表示恒温系统开启后阶段，双曲线的一部分CD表示恒温系统关闭阶段．请根据图中信息解答下列问题： （1）求这天的温度y与时间x（0≤x≤5）的函数关系式； （2）求恒温系统设定的恒定温度； （3）若大棚内的温度低于10℃不利于新品种水果的生长，问这天内，相对有利于水果生长的时间共多少小时？ 参考答案 题号 1 2 3 4 5 答案 D C B B B 选择题 二、填空题 1．【解答】解：由图象，函数y1＝2x和的交点横坐标为﹣1，1， ∴当﹣1＜x＜0或x＞ ... ...