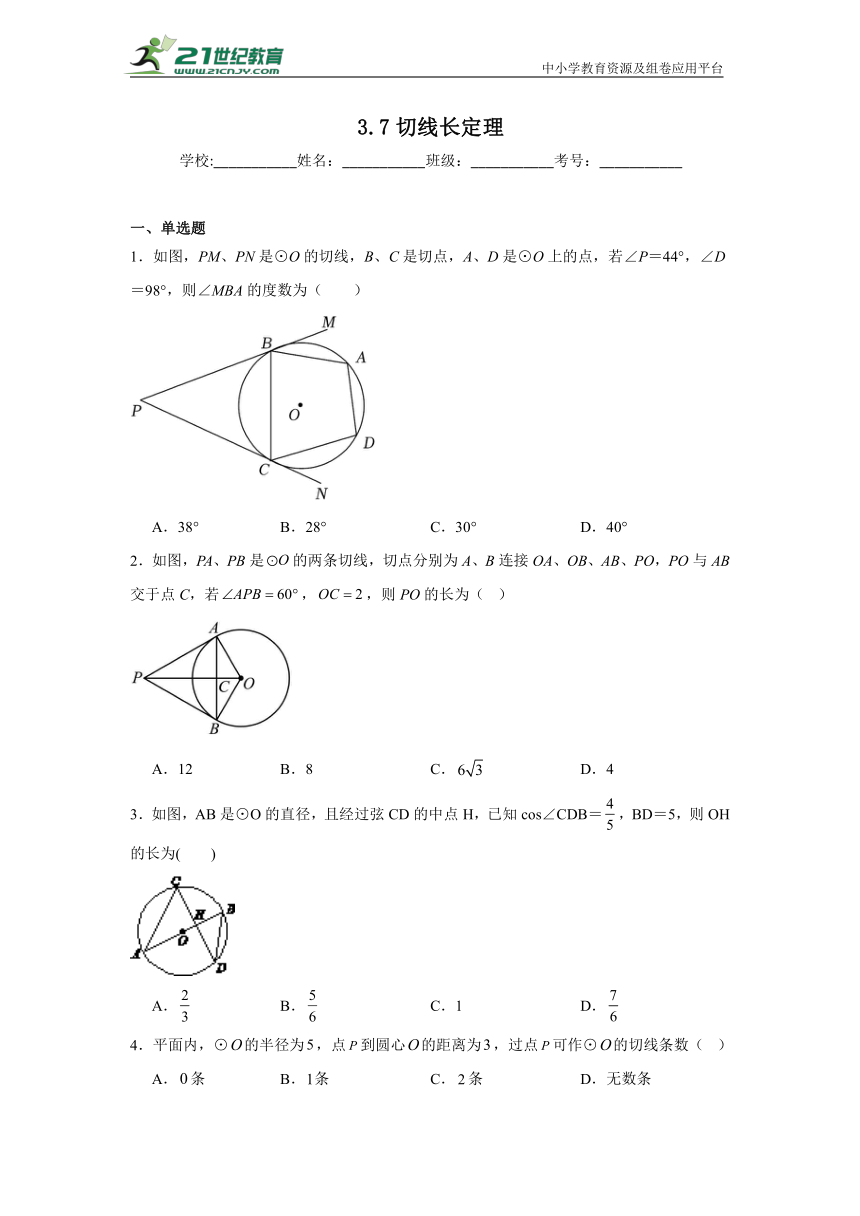
中小学教育资源及组卷应用平台 3.7切线长定理 学校:_____姓名:_____班级:_____考号:_____ 一、单选题 1.如图,PM、PN是⊙O的切线,B、C是切点,A、D是⊙O上的点,若∠P=44°,∠D=98°,则∠MBA的度数为( ) A.38° B.28° C.30° D.40° 2.如图,PA、PB是的两条切线,切点分别为A、B连接OA、OB、AB、PO,PO与AB交于点C,若,,则PO的长为( ) A.12 B.8 C. D.4 3.如图,AB是⊙O的直径,且经过弦CD的中点H,已知cos∠CDB=,BD=5,则OH的长为( ) A. B. C.1 D. 4.平面内,⊙的半径为,点到圆心的距离为,过点可作⊙的切线条数( ) A.条 B.条 C.条 D.无数条 5.如图,⊙O是的内切圆,点D、E分别为边上的点,且为⊙O的切线,若的周长为,的长是,则的周长是( ) A.7 B.8 C.9 D. 6.如图,是的直径,分别是的中点,在上.下列结论:①;②;③四边形是正方形;④.其中正确的结论有( ) A.1个 B.2个 C.3个 D.4个 7.若O是△ABC的内心,且∠BOC=100°,则∠A=( ) A.20° B.30° C.50° D.60° 8.如图,∠ACB=60○,半径为1的⊙O切BC于点C,若将⊙O在直线CB上沿某一方向滚动,当滚动到⊙O与CA也相切时,圆心O移动的水平距离为( ) A. B. C.π 或 D.或 9.若的外接圆半径为R,内切圆半径为,则其内切圆的面积与的面积比为( ) A. B. C. D. 10.如图,PA、PB为圆O的切线,切点分别为A、B,PO交AB于点C,PO的延长线交圆O于点D,下列结论不一定成立的是( ) A.PA=PB B.∠BPD=∠APD C.AB⊥PD D.AB平分PD 11.如图,O的半径为1,弦AB=1,点P为优弧AB上一动点,AC⊥AP交直线PB于点C,则△ABC的最大面积是( ) A. B. C. D. 12.如图,等边三角形ABC和正方形ADEF都内接于,则( ) A. B. C. D. 二、填空题 13.如图,⊙O是△ABC的内切圆,⊙O切BC于点D,BD=3,CD=2,△ABC的周长为14,则AB= . 14.如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CB,CA分别相交于点E,F,则线段EF长度的最小值是 . 15.如图,的周长为16,是的内切圆,若,,则的长为 . 16.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D.AD与BC相交于点F,连结BE,DC,已知EF=2,CD=5,则AD= . 17.如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D、E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为4cm,则Rt△MBN的周长为 cm. 三、解答题 18.在平面直角坐标系中,若点和点关于轴对称,点和点关于直线对称,则称点是点关于轴,直线的二次对称点. (1)如图1,点; ①若点是点关于轴,直线的二次对称点,则点的坐标为_____; ②点是点关于轴,直线的二次对称点,则的值为_____; ③点是点关于轴,直线的二次对称点,则直线的表达式为_____; (2)如图2,的半径为1.若上存在点,使得点是点关于轴,直线的二次对称点,且点在射线上,求的取值范围; (3)是轴上的动点,的半径为2,若上存在点,使得点是点关于轴,直线的二次对称点,且点在轴上,写出的取值范围. 19.李老师在上课时的屏幕上有如下内容:如图,是的直径,点C为弧的中点,连结交于点E,,老师要求同学们在矩形方框中添加一个条件和结论后,编制成一道完整的题目,并解答. (1)李老师在方框中添加的内容是“,求的长”,请你解答; (2)某同学加的内容是,连C,求的值”.请你帮该同学完成解答. 20.已知为的外接圆,. (1)如图1,延长至点,使,连接. ①求证:为直角三角形; ②若的半径为4,,求的值; (2)如图2,若,为上的一点,且点,位于两侧,作关于对称的图形,连接,试猜想,,三者之间的数量关系并给予证明. 2 ... ...
~~ 您好,已阅读到文档的结尾了 ~~