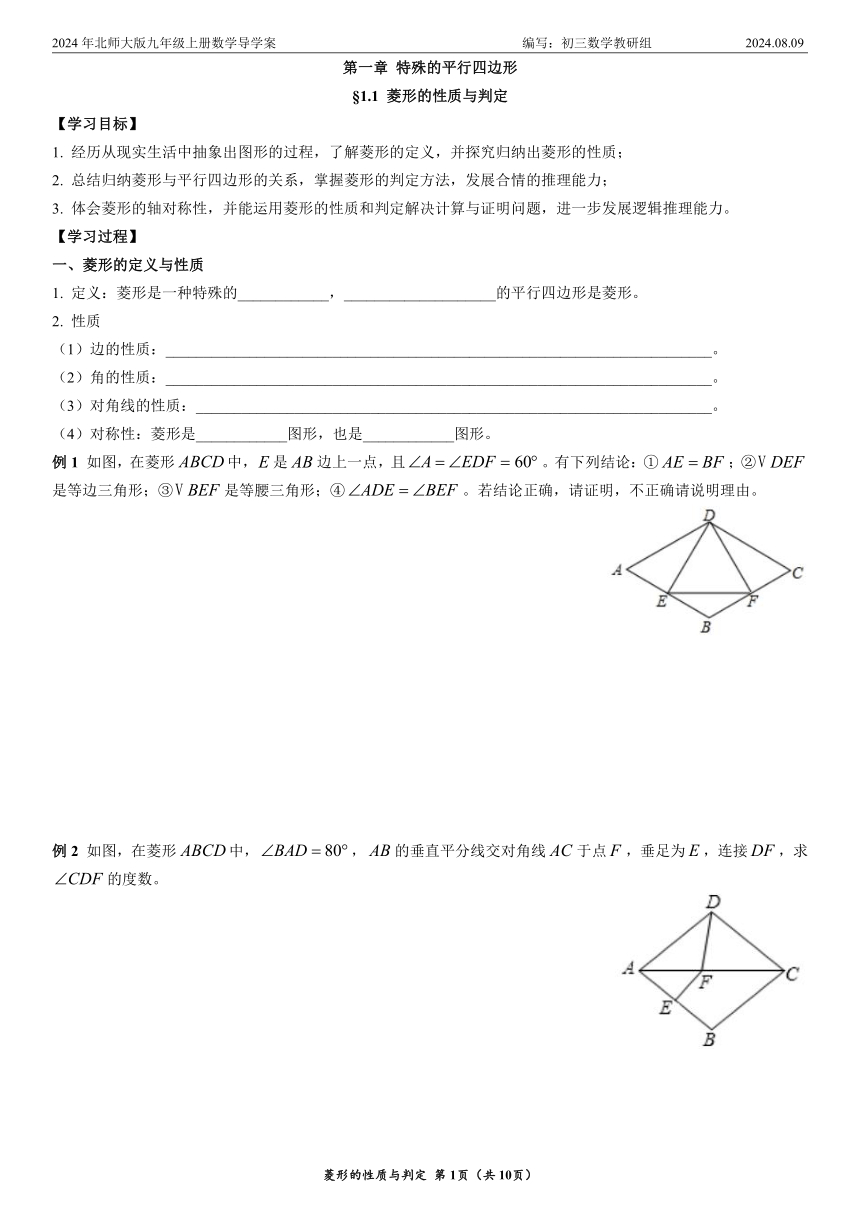
2024年北师大版九年级上册数学导学案 编写:初三数学教研组 2024.08.09 第一章 特殊的平行四边形 §1.1 菱形的性质与判定 【学习目标】 1. 经历从现实生活中抽象出图形的过程,了解菱形的定义,并探究归纳出菱形的性质; 2. 总结归纳菱形与平行四边形的关系,掌握菱形的判定方法,发展合情的推理能力; 3. 体会菱形的轴对称性,并能运用菱形的性质和判定解决计算与证明问题,进一步发展逻辑推理能力。 【学习过程】 一、菱形的定义与性质 1. 定义:菱形是一种特殊的_____,_____的平行四边形是菱形。 2. 性质 (1)边的性质:_____。 (2)角的性质:_____。 (3)对角线的性质:_____。 (4)对称性:菱形是_____图形,也是_____图形。 例1 如图,在菱形中,是边上一点,且。有下列结论:①;②是等边三角形;③是等腰三角形;④。若结论正确,请证明,不正确请说明理由。 例2 如图,在菱形中,,的垂直平分线交对角线于点,垂足为,连接,求的度数。 例3 已知四边形是边长为2的菱形,,对角线与交于点,过点的直线交于点,交于点。 (1)求证:; (2)若,求的长。 [识记理解1] 1. 如图,菱形的对角线、相交于点,,,过点作,垂足为,求点到边的距离的长度。 2. 如图,菱形中,,于点,,连接,求的度数。 3. 如图,在菱形中,,分别在,上,且,与交于点,连接。若,求的度数。 4. 如图,四边形是菱形,过的中点作的垂线,交于点,交的延长线于点。 (1)求证:; (2)若,求菱形的周长。 二、菱形的判定 1. 平行四边形判定方法 (1)边的关系:_____的平行四边形是菱形。 (2)对角线的关系:_____的平行四边形是菱形。 2. 四边形判定方法 (1)边的关系:_____的四边形是菱形。 (2)对角线的关系:_____的四边形是菱形。 例4 如图,在中,,于,平分,分别于、交于、,于。连接,求证:四边形是菱形。 例5 如图,在中,,分别是边,上的点,且,直线分别交的延长线、的延长线于点,,交于点。 (1)求证:; (2)连接,若,则四边形是什么特殊四边形?请说明理由。 [识记理解2] 1. 如图,矩形的对角线相交于点,,。求证:四边形是菱形。 2. 如图,在矩形中,对角线的垂直平分线与交于点,与交于点,连接,。 (1)求证:四边形是菱形; (2)若,,求的长。 三、菱形性质与判定的综合应用 1. 面积问题(等面积原理):菱形的面积既可以用_____的面积公式,也可以用_____求算。 2. 折叠问题(全等原理):折叠前后的图形是_____的,是完全对称的。 3. 最值问题(对称原理) (1)线段和的最小值:做对称点后,连接后一般运用两点之间_____最短(线段之中_____最短定理)解决。 (2)动线段的最小值:运用转化和运动的思想,转换到一般模型中,如三角形的第三边长_____。 (3)利用菱形的对称性:菱形既是_____图形,也是_____图形。 例6 如图,在菱形中,,对角线。若过点作,垂足为,求的长。 例7 将矩形纸片按如图所示的方式折叠,得到菱形。若,求的长。 例8 如图,在对角线长分别为12和16的菱形中,、分别是边、的中点,是对角线上的任意一点,求的最小值。 例9 如图,在边长为2的菱形中,,是边的中点,是边上的一动点,将沿所在直线翻折得到,连接,求长度的最小值。 [识记理解3] 1. 如图,已知菱形中,,,过线段上的一个动点(不与、重合)分别向直线、作垂线,垂足分别为、。 (1)求的长; (2)连接,当取得最小值时,求此时的长。 2. 如图,在菱形中,,,点是菱形内部一点,且满足,求的最小值。 【知能提升】 一、选择题 1. 已知四边形的对角线相等,顺次连接四边形的四条边中点,得到的新四边形的形状是( ) A. 平行四边形 B. 矩形 C. 菱形 D. 正方形 2. 下列条件中,能判定平行四边形是菱形的是 ... ...
~~ 您好,已阅读到文档的结尾了 ~~