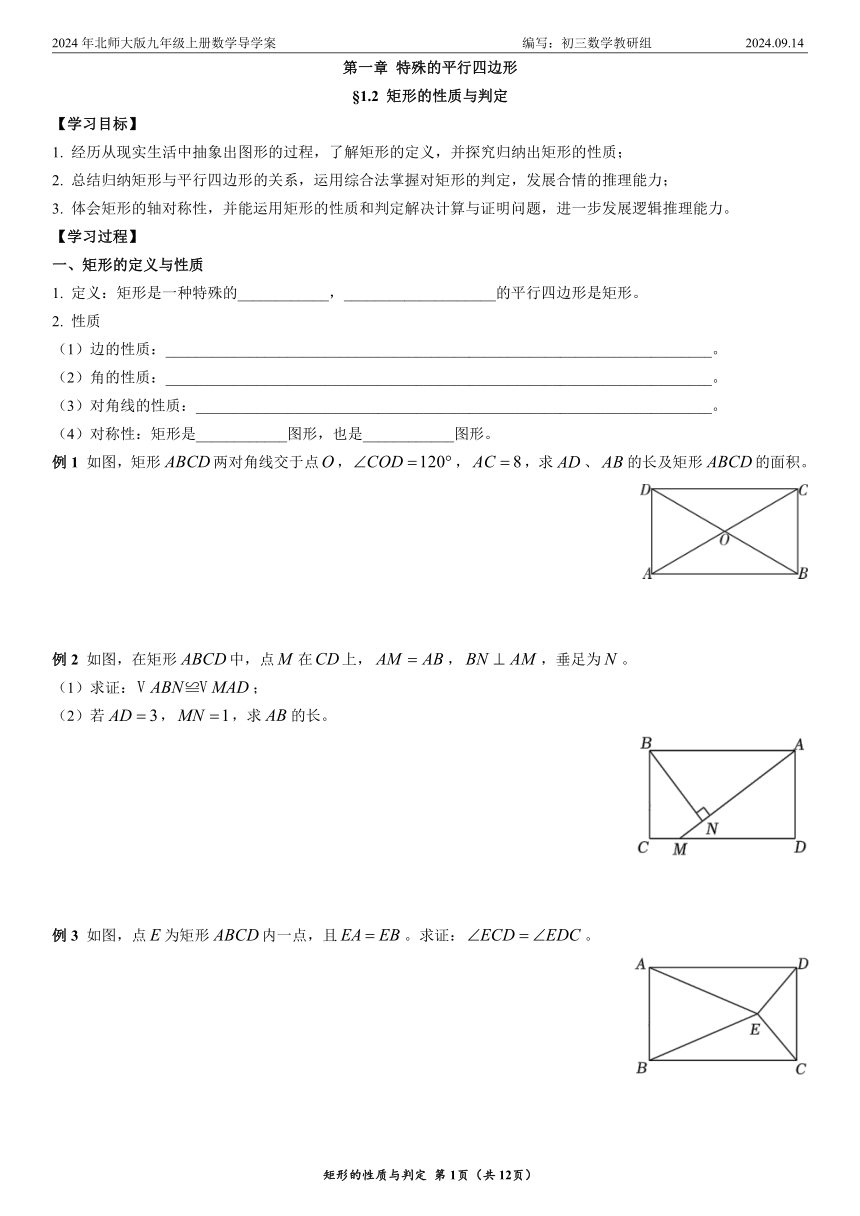
2024年北师大版九年级上册数学导学案 编写:初三数学教研组 2024.09.14 第一章 特殊的平行四边形 §1.2 矩形的性质与判定 【学习目标】 1. 经历从现实生活中抽象出图形的过程,了解矩形的定义,并探究归纳出矩形的性质; 2. 总结归纳矩形与平行四边形的关系,运用综合法掌握对矩形的判定,发展合情的推理能力; 3. 体会矩形的轴对称性,并能运用矩形的性质和判定解决计算与证明问题,进一步发展逻辑推理能力。 【学习过程】 一、矩形的定义与性质 1. 定义:矩形是一种特殊的_____,_____的平行四边形是矩形。 2. 性质 (1)边的性质:_____。 (2)角的性质:_____。 (3)对角线的性质:_____。 (4)对称性:矩形是_____图形,也是_____图形。 例1 如图,矩形两对角线交于点,,,求、的长及矩形的面积。 例2 如图,在矩形中,点在上,,,垂足为。 (1)求证:; (2)若,,求的长。 例3 如图,点为矩形内一点,且。求证:。 [识记理解1] 1. 如图,矩形的周长为18 cm,是的中点,且,求矩形两邻边的长。 2. 如图,在矩形中,为边的中点,连接,的延长线和的延长线相交于点。 (1)求证:; (2)连接,与相交于点,若△的面积为2,求矩形的面积。 3. 如图,在矩形中,是对角线的中点,过点作分别交,于点,。 (1)求证:; (2)若,,求的长。 4. 如图,在矩形中,,对角线与相交于点,,垂足为,。求的长。 二、矩形的判定 1. 平行四边形判定方法 (1)角的关系:_____的平行四边形是矩形。 (2)对角线的关系:_____的平行四边形是矩形。 2. 四边形判定方法 (1)角的关系:_____的四边形是矩形。 例4 如图,在平行四边形中,过点作于点,点在边上,且,连接、。 (1)求证:四边形是矩形; (2)若平分,,,求的长。 例5 如图,等腰中,,、分别是边、上的中线,与相交于点,点,分别为线段和的中点。求证:四边形是矩形。 例6 如图,在中,,是△的一条角平分线,是△外角的平分线,,垂足为点。 (1)求证:四边形为矩形; (2)连接,交于点,请判断四边形的形状,并证明; (3)线段与有怎样的关系?请写出你的结论,并证明。 [识记理解2] 1. 如图,在中,的平分线交于点,的平分线交于点,连接。 (1)求证:; (2)若,求证:四边形是矩形。 2. 如图,在四边形中,、相交于点,,,。 (1)如图1,求证:四边形为矩形; (2)如图2,是边上任意一点,,,、分别是垂足,若,,求的值。 3. 如图,直线与交于点,,分别是和的平分线,于点,于点。求证:四边形是矩形。 4. 如图,在菱形中,对角线,相交于点,是中点,连接。过点作交的延长线于点,连接。求证:(1);(2)四边形是矩形。 三、矩形性质与判定的综合应用 1. 折叠问题(全等原理):折叠前后的图形是_____的,是完全对称的。 2. 动点问题 (1)在直角三角形中,注意特殊的角度和边,同时直角三角形斜边上的中点_____。 (2)利用矩形的对称性:矩形既是_____图形,也是_____图形。 例7 如图,四边形是矩形,把矩形沿折叠,点落在点处,与的交点为,连接。求证:(1);(2)。 例8 如图,在矩形中,cm,、、、分别从、、、出发沿、、、方向在矩形的边上同时运动,当有一个点先到达所在运动边的另一个端点时即停止,已知在相同时间内,若cm(),则cm,cm,cm。 (1)当为何值时,点的运动停止; (2)点与点可能相遇吗?点与点呢?请通过计算说明理由; (3)当为何值时,以、Q、、为顶点的四边形是平行四边形? 例9 如图,在中,为边上的一点,是的中点,过点作的平行线交的延长线于点,且。连接。 (1)与有什么数量关系?请说明理由; (2)当满足什么条件时,四边形是矩形?并说明理由。 [识记理解3] 1. 如图,将矩形纸片折叠,使点与点重合 ... ...
~~ 您好,已阅读到文档的结尾了 ~~