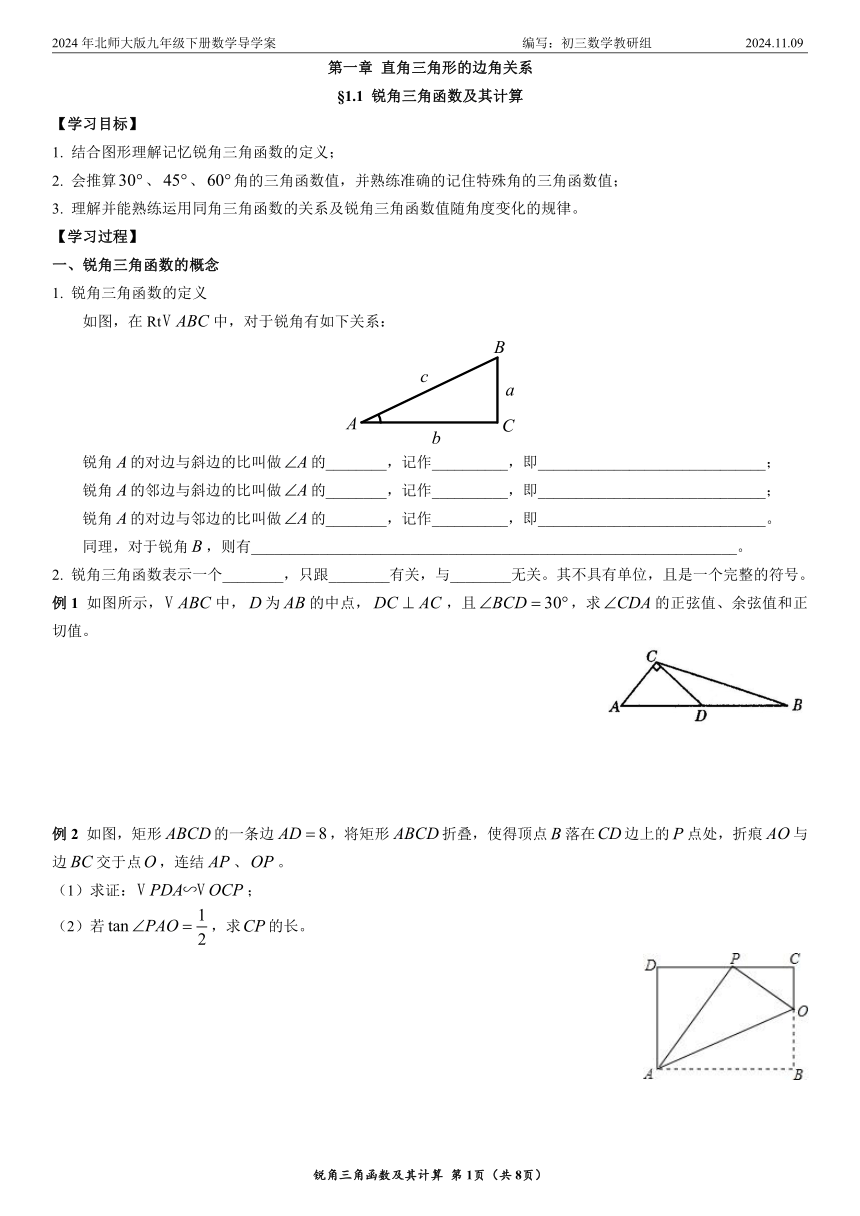
2024年北师大版九年级下册数学导学案 编写:初三数学教研组 2024.11.09 第一章 直角三角形的边角关系 §1.1 锐角三角函数及其计算 【学习目标】 1. 结合图形理解记忆锐角三角函数的定义; 2. 会推算、、角的三角函数值,并熟练准确的记住特殊角的三角函数值; 3. 理解并能熟练运用同角三角函数的关系及锐角三角函数值随角度变化的规律。 【学习过程】 一、锐角三角函数的概念 1. 锐角三角函数的定义 如图,在Rt中,对于锐角有如下关系: 锐角的对边与斜边的比叫做的_____,记作_____,即_____; 锐角的邻边与斜边的比叫做的_____,记作_____,即_____; 锐角的对边与邻边的比叫做的_____,记作_____,即_____。 同理,对于锐角,则有_____。 2. 锐角三角函数表示一个_____,只跟_____有关,与_____无关。其不具有单位,且是一个完整的符号。 例1 如图所示,中,为的中点,,且,求的正弦值、余弦值和正切值。 例2 如图,矩形的一条边,将矩形折叠,使得顶点落在边上的点处,折痕与边交于点,连结、。 (1)求证:; (2)若,求的长。 例3 如图,格点图中每个小正方形的边长都是1,的顶点,,都在格点上,求的正弦值、正切值和余弦值。 [识记理解1] 1. 如图所示,在矩形中,是边上的点,,,垂足为,连接。 (1)求证:;(2)若,,求的值。 2. 如图,格点图中每个小正方形的边长都是1,的顶点,,都在格点上,求。 3. 如图,在直角坐标平面内,为原点,点的坐标为,点在第一象限内,,。求点的坐标及的正弦值、正切值和余弦值。 二、特殊角的三角函数值 锐角α 规律: (1)正弦、正切值随锐角度数的增大(或减小)而_____;余弦值随锐角度数的增大(或减小)而_____。 (2)对于一个锐角而言,正弦、余弦、正切值的符号都是_____。 例4 求下列各式的值。 (1); (2); (3)。 [识记理解2] 1. 计算下列各式的值:(1);(2)。 三、锐角三角函数的关系 1. 互余关系:_____;_____; 2. 平方关系:_____; 3. 倒数关系:_____或_____; 4. 商数关系:_____。 例5 已知中的与满足。 (1)试判断的形状; (2)求的值。 例6 按照下列要求填空。 (1)已知为锐角,,那么_____。 (2)_____(填写不等号) (3)_____=_____; (4)_____=_____; (5)_____,_____(α为锐角)。 [识记理解3] 1. 在中,若,、都是锐角,则的度数为多少? 2. 解方程:(是锐角) 四、锐角三角函数的几何应用 1. 坡度:坡面的_____高度和_____高度之比叫做坡度,用符号____表示,即_____。 2. 一次函数的斜率 (1)倾斜角的定义:在平面直角坐标系中,_____的一次函数直线和_____所围成的角即直线的倾斜角。 (2)斜率的定义:用以刻画直线的_____,用符号____表示。对于直线而言,斜率可表示为两点的_____,即_____。 (3)倾斜角和斜率之间的关系:_____。当倾斜角是锐角时,随着倾斜角的增大,斜率会_____(斜率的符号都是_____),即直线越_____。 例7 求下列直线的倾斜角和斜率:(1);(2);(3) [识记理解4] 1. 如图,在平面直角坐标系中,直线与轴交于点,与轴交于点,直线与轴交于点,与直线交于,,。求直线、的解析式。 【知能提升】 一、选择题 1. 如图,在Rt中,,于点,则下列结论不正确的是( ) A. B. C. D. 第1题图 第2题图 2. 如图在网格中,小正方形的边长均为1,点,,都在格点上,则的正切值是( ) A. 2 B. C. D. 3. 如图,在中,,,,则的值是( ) A. B. C. D. 第3题图 第4题图 4. 如图,在Rt中,,于点,若,,则的值为( ) A. B. C. D. 5. 在Rt中,,若将各边长度都扩大为原来的2倍,则的正弦值( ) A. 扩大2倍 B. 缩小2倍 C. 扩大4倍 D. 不变 6. 已知,,则的值是( ) A. B. C. D. 7. 在Rt中,, ... ...
~~ 您好,已阅读到文档的结尾了 ~~