中考复习模型3：三角形中的辅助线模型（PDF，无练习）

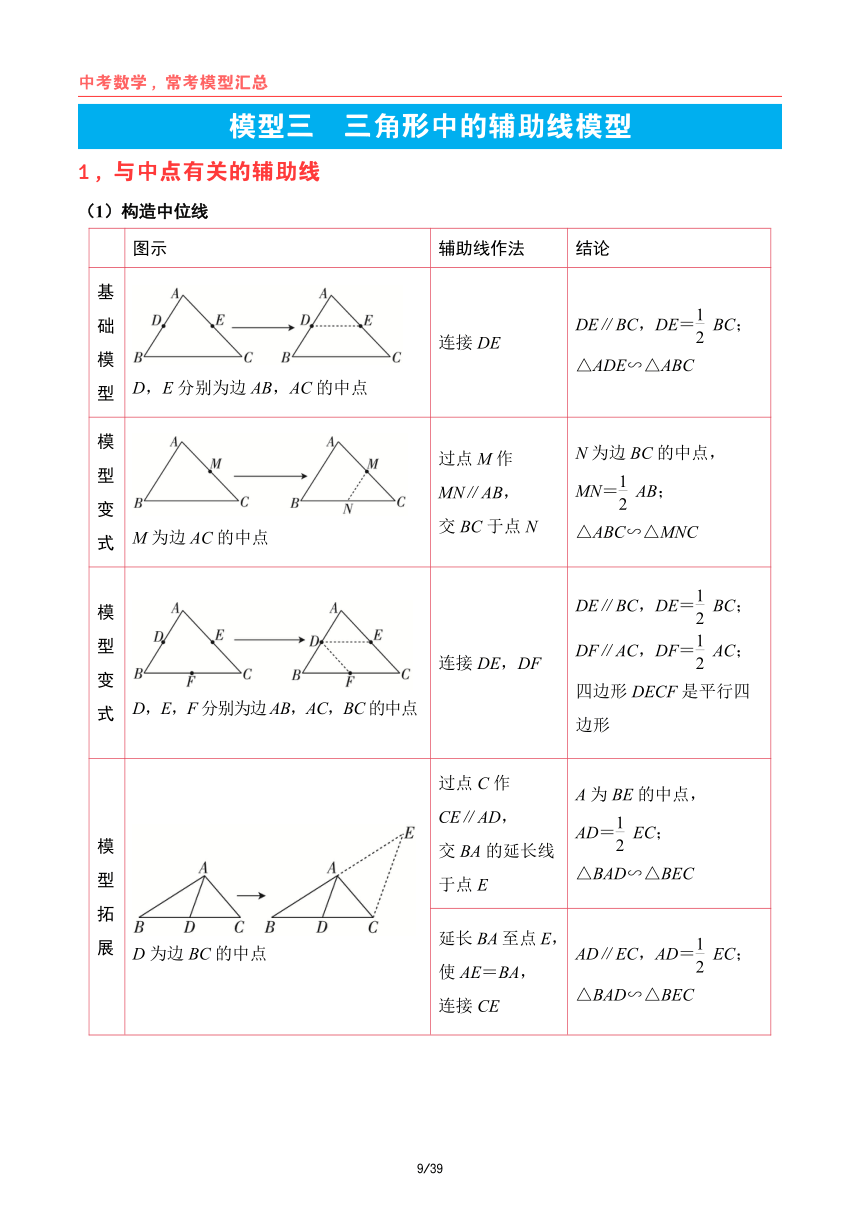
中考数学，常考模型汇总 模型三 三角形中的辅助线模型 1，与中点有关的辅助线 （1）构造中位线 图示 辅助线作法 结论 基 DE BC DE 1础 ∥ ， ＝ BC； 连接 DE 2 模 △ADE∽△ABC 型 D，E分别为边 AB，AC的中点 模 过点 M作 N为边 BC的中点， 型 MN 1∥AB， MN＝ AB； 变 2 M 交 BC于点 N式 为边 AC的中点 △ABC∽△MNC 1 模 DE∥BC，DE＝ BC；2 型 DF AC DF 1∥ ， ＝ AC； 连接 DE，DF 2 变 四边形 DECF是平行四 式 D，E，F分别为边AB，AC，BC的中点 边形 过点 C作 A为 BE的中点， CE∥AD， AD 1＝ EC； 模 交 BA的延长线 2 型 E △BAD∽△BEC于点 拓 延长 BA至点 E， 展 D为边 BC的中点 AD∥EC，AD 1＝ EC； 使 AE＝BA， 2 CE △BAD∽△BEC连接 9/39 中考数学，常考模型汇总 （2）构造中线 图示 辅助线作法 结论 等腰三 角形底 BD＝CD 1＝ BC，2 边中线 连接 AD AD⊥BC， （三线 AD平分∠BAC AB＝AC，D为边 BC的中点 合一） 直角三 1 角形斜 连接 CD CD＝AD＝BD＝ AB2 边中线 ∠ACB＝90°，D为边 AB的中点 （3）倍长（类）中线构造全等三角形 △ADC≌△EDB， 延长 AD到点 基础 ∠DBE＝∠C， E，使 DE＝ 模型 ∠E＝∠CAD， AD，连接 BE BE＝CA，BE∥CA D为边 BC的中点 △BDE≌△CDF， 延长 ED到点 模型 ∠B＝∠DCF， F，使 DF＝ 变式 ∠BED＝∠F， ED，连接 CF BE＝CF，AB∥CF D为边 BC的中点，E为边 AB上任意一点 10/39 中考数学，常考模型汇总 2，与角平分线有关的辅助线 图示 辅助线作法 结论 PA＝PB， 过点 P作 作垂 Rt△OAP≌Rt△O PB⊥ON 线，构 BP 造全 P是∠MON的平分线上一点，PA⊥OM 等、等 △OAB是等腰三角 腰三角 延长 AP交ON 形，PA＝PB， 形 于点 B Rt△OPA≌Rt△OP P是∠MON的平分线上一点，AP⊥OP B 作平行 过点 P作 线，构 △OPQ是等腰三 PQ∥ON交 造等腰 角形，OQ＝PQ OM于点 Q 三角形 P是∠MON的平分线上一点 截长法：在 BA △BDE≌△BDC， 上取 BE＝BC， DE＝DC 截长补 连接 DE 在△ABC中，BD平分∠ABC 短，构 造全等 三角形 补短法：延长 △BAD≌△BED， BC到点 E，使 DA＝DE BE＝BA 在△ABC中，BD平分∠ABC 11/39