中考复习模型4：面积模型（PDF，无练习）

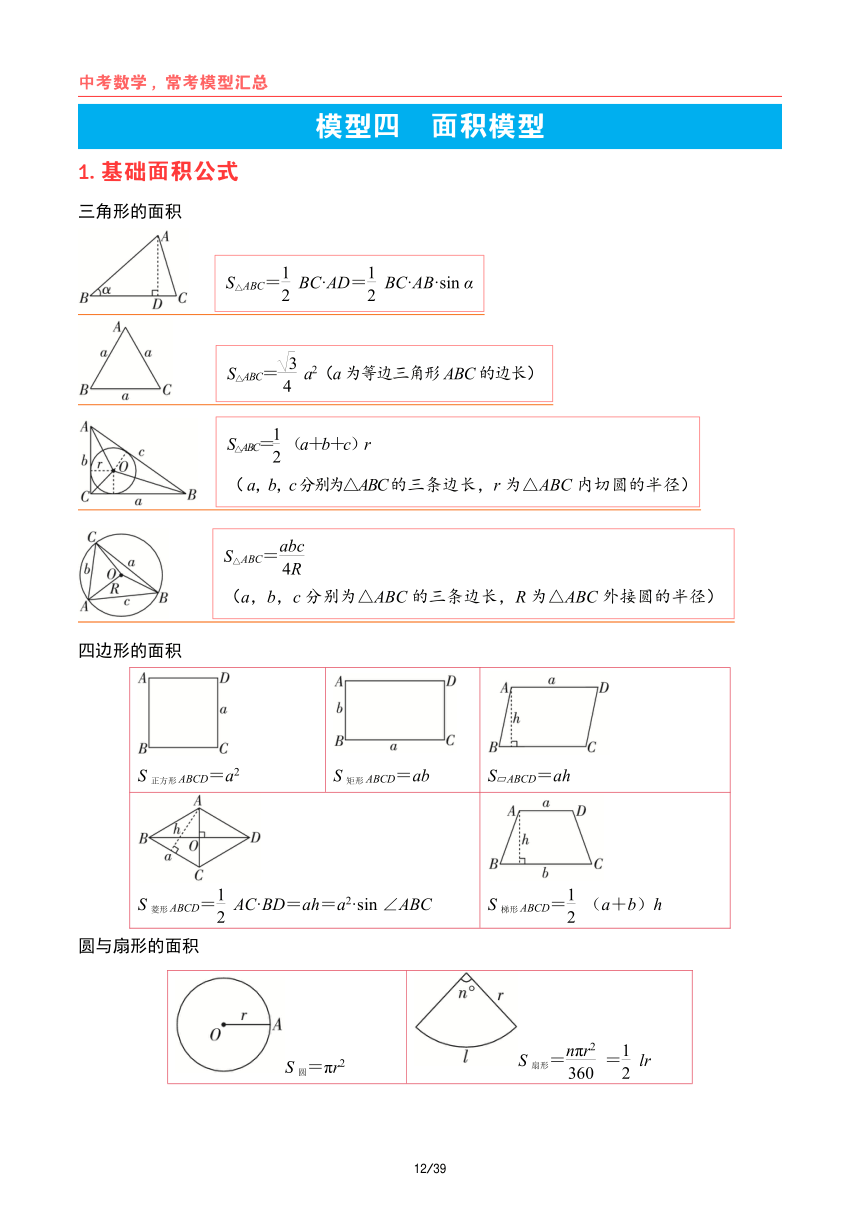
中考数学，常考模型汇总 模型四 面积模型 1. 基础面积公式 三角形的面积 S 1 1△ABC＝ BC·AD＝ BC·AB·sin α2 2 S 3△ABC＝ a2（a为等边三角形ABC的边长）4 S 1△ABC＝ （a＋b＋c）r2 （ a，b，c分别为△ABC的三条边长，r为△ABC内切圆的半径） S abc△ABC＝ 4R （a，b，c分别为△ABC的三条边长，R为△ABC外接圆的半径） 四边形的面积 S 2正方形 ABCD＝a S 矩形 ABCD＝ab S ABCD＝ah S 1 1菱形 ABCD＝ AC·BD＝ah＝a2·sin∠ABC S 梯形 ABCD＝ （a＋b）h2 2 圆与扇形的面积 nπr2 1 S ＝πr2 S 扇形＝ ＝ lr圆 360 2 12/39 中考数学，常考模型汇总 2.求阴影部分的面积 （1）公式法 若所求阴影部分面积是一个规则的图形，如三角形、特殊四边形、扇形等，可直接利用面 积公式求解 （2）和差法 直接和差法（无需辅助线） S 阴影＝S△ABC－S S 阴影＝S 扇形 AOB－S△OCD－S 正方形CDEF 扇形DAF S 阴影＝S ABCD－S 扇形DAE－S△BCE S 阴影＝S△ABC＋S 扇形 CAE－S 扇形 BAD 构造和差法（需作辅助线） S 阴影＝S△BOD＋S 扇形 COD S 阴影＝S△ODC－S 扇形DOE S 阴影＝S 扇形 AOB－S△AOB S 阴影＝S△BCE＋S 扇形 ABE－S 扇形CBF 13/39 中考数学，常考模型汇总 （3）等积转化法 当所求的阴影部分是一个不规则的图形，直接求面积较复杂或无法计算时，可通过平移、 对称、割补等方法，将所求图形进行转化，再利用公式法或和差法计算转化后的图形面积． S 阴影＝S 扇形 BOC S 阴影＝S△ACD S 阴影＝S 扇形 COD S 阴影＝S 扇形DOE （4）组合法 πa2S a2 S πa 2 阴影＝ － 阴影＝ －a22 2 （a为正方形 ABCD的边长） （a为正方形 ABCD的边长） 14/39 中考数学，常考模型汇总 3.平面直角坐标系中的面积模型 （1）求三角形面积 S 1△ABC＝ |xA－xB|·|yC－yA|2 S 1△ABC＝ |yA－yB|·|xC－x2 A | S△ABC＝S 1 1 △ADB＋S△CDB＝ BD·（AE＋CF）＝ |xB－xD|·|yC－yA|2 2 S 1 1△ABC＝S△ADB＋S△CDB＝ BD·（AE＋CF）＝ |y －y |·|x －x |2 2 D B C A 15/39 中考数学，常考模型汇总 （3）与二次函数有关的线段、面积最值问题 求铅垂线 CD的最大值： 设 C（m，km＋b1），则 D（m，am2＋bm＋c）. CD＝|km＋b1－am2－bm－c| 求垂线段 DE的最大值： 设 C（m，km＋b1），则 D（m，am2＋bm＋c）. CD＝|km＋b1－am2－bm－c|. DE＝CD·cos∠CDE （一般通过证明可得到∠CDE是特殊角） 求△ABD的面积的最大值： 设 C（m，km＋b1），则 D（m，am2＋bm＋c）. CD＝|km＋b1－am2－bm－c|. S 1△ABD＝ CD·|xB－xA|2 （4）等面积模型 问题：已知 A，B为抛物线与 x轴的交点，C为抛物线上一点，连接 BC交 y轴于点 D，在 抛物线上找一点 P，使得 S△BCP＝S△ABC. 解法：过点 A作 BC的平行线，交抛物线于点 P1，交 y轴于点 E，在点 D下方的 y轴上找 一点 F，使得 DF＝DE，过点 F作 BC的平行线，交抛物线于点 P2，P3，则点 P1，P2，P3 即为所求。 16/39 ... ...