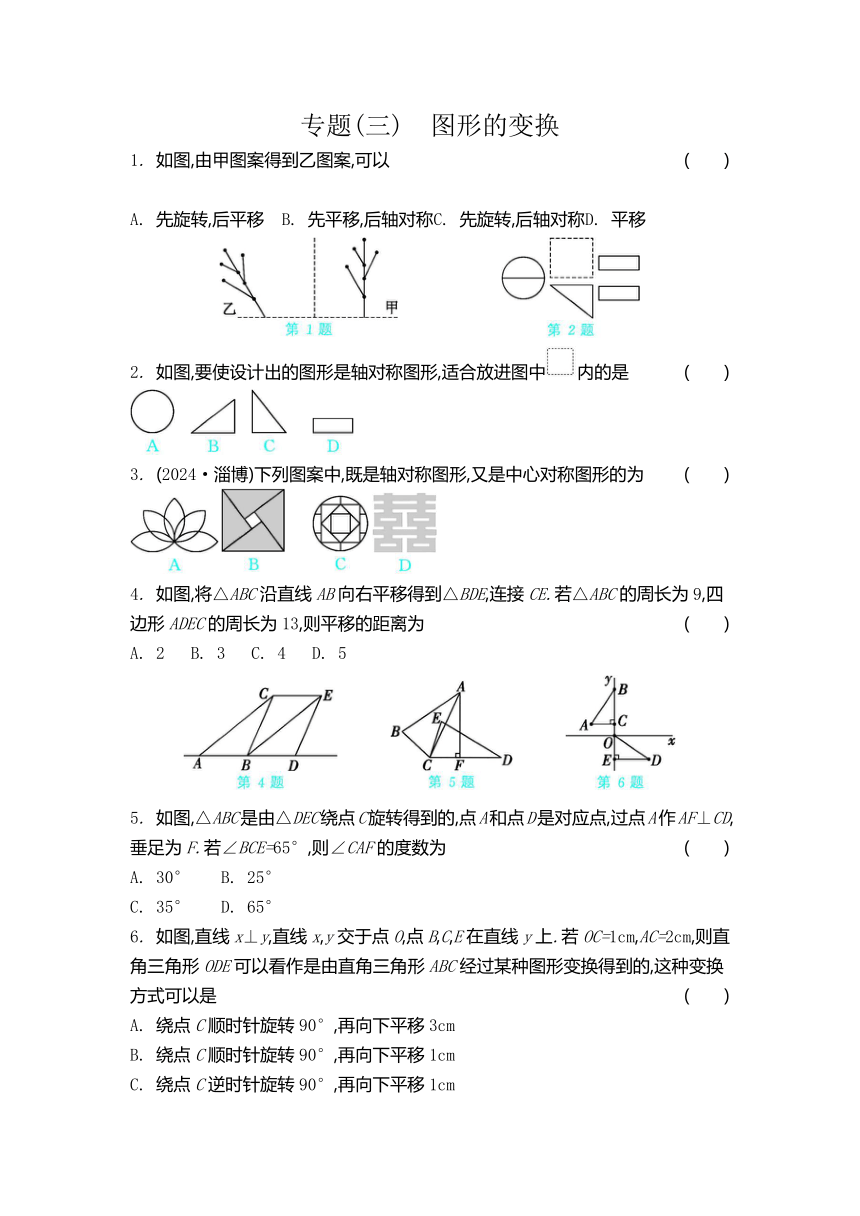
专题(三) 图形的变换 1. 如图,由甲图案得到乙图案,可以 ( ) A. 先旋转,后平移 B. 先平移,后轴对称 C. 先旋转,后轴对称 D. 平移 2. 如图,要使设计出的图形是轴对称图形,适合放进图中内的是 ( ) 3. (2024·淄博)下列图案中,既是轴对称图形,又是中心对称图形的为 ( ) 4. 如图,将△ABC沿直线AB向右平移得到△BDE,连接CE.若△ABC的周长为9,四边形ADEC的周长为13,则平移的距离为 ( ) A. 2 B. 3 C. 4 D. 5 5. 如图,△ABC是由△DEC绕点C旋转得到的,点A和点D是对应点,过点A作AF⊥CD,垂足为F.若∠BCE=65°,则∠CAF的度数为 ( ) A. 30° B. 25° C. 35° D. 65° 6. 如图,直线x⊥y,直线x,y交于点O,点B,C,E在直线y上.若OC=1cm,AC=2cm,则直角三角形ODE可以看作是由直角三角形ABC经过某种图形变换得到的,这种变换方式可以是 ( ) A. 绕点C顺时针旋转90°,再向下平移3cm B. 绕点C顺时针旋转90°,再向下平移1cm C. 绕点C逆时针旋转90°,再向下平移1cm D. 绕点C逆时针旋转90°,再向下平移3cm 7. 如图,△ABC与△CDA关于点O对称,过点O任意作一直线EF分别交AD,BC于点E,F.有下列结论:① 点E和点F,点B和点D分别关于点O对称;② 直线BD必经过点O;③ △AOE与△COF成中心对称;④ 四边形DEOC与四边形BFOA的面积必相等.其中,正确的个数为 ( ) A. 1 B. 2 C. 3 D. 4 8. (2023·苏州市区期中)如图,将△ABC沿水平方向向右平移到△DEF的位置.若BF=11,EC=5,则A,D之间的距离等于 . 9. 将如图所示的一张左右对折后的长方形纸片按图中虚线剪下来,然后铺开后的图案是汉字 . 10. 线段AB与线段AC关于点A成中心对称,则A,B,C三点的位置关系是 . 11. (2024·镇江)如图,△ABC的边AB的垂直平分线交AC于点D,连接BD.若AC=8,CD=5,则BD的长为 . 12. 如图,在4×4的网格图中,每个小正方形的顶点称为格点,左上角的涂色部分是一个以格点为顶点的格点正方形.若再作一个格点正方形,并涂色,使这两个格点正方形无重叠部分,且组成的图形既是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有 种. 13. 用等腰直角三角尺画∠AOB=45°,并将三角尺沿OB方向平移到如图所示的虚线处后绕点M按逆时针方向旋转22°,则三角尺的斜边与射线OA的夹角α的度数为 °. 14. 如图,在直角三角形ABC中,∠ACB=90°,∠B=30°.根据尺规作图的痕迹可知,∠ADE的度数为 . 15. 如图,在直角三角形ABC中,AC=3,BC=4,AB=5,点C,A在直线l上,将△ABC绕点A顺时针旋转到位置①,得到点P1,点P1在直线l上,将位置①的三角形绕点P1顺时针旋转到位置②,得到点P2,点P2在直线l上……按照此规律继续旋转,直到得到点P2025,则AP2025的长为 . 16. 在实际生活中,轴对称图形无处不在.请你以给定的图形“○○”“△△”“”为构件,尽可能多地构思出独特且有实际生活意义的轴对称图形,并进行说明. 17. (2024·广州改编)如图,在△ABC中,∠B=90°. (1) 尺规作图:作AC边上的中点O,连接BO(保留作图痕迹,不写作法). (2) 在(1)中所作的图内,将线段BO绕点O逆时针旋转180°得到DO,连接AD,CD.比较大小:AB CD,∠ADC 90°(填“>”“<”或“=”). 18. (2023·张家港期中)如图,在10×10的正方形网格中,每个小正方形的边长均为1,△ABC是格点三角形(顶点是网格线的交点).将△ABC先向左平移3格,再向上平移4格得到△A'B'C',点A,B,C的对应点分别是A',B',C'. (1) 在图中画出平移后的△A'B'C',连接BB',BC'; (2) △BB'C'的面积为 ; (3) AC与A'C'的关系为 ; (4) 设∠A'B'C'=α,∠BC'B'=β,∠ABC'=γ,则α,β,γ之间满足的等量关系是 . 专题(三) 图形的变换 1. A 2. ... ...
~~ 您好,已阅读到文档的结尾了 ~~