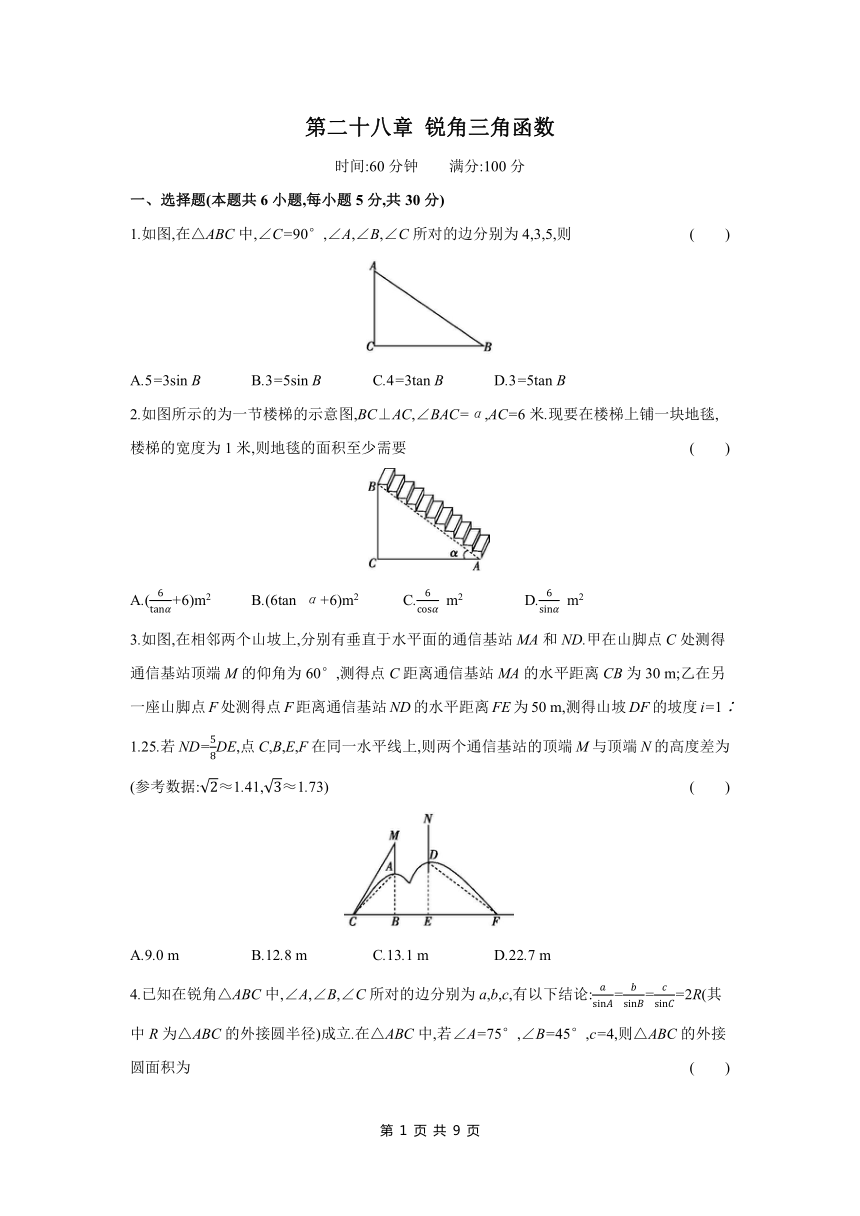
第二十八章 锐角三角函数 时间:60分钟 满分:100分 一、选择题(本题共6小题,每小题5分,共30分) 1.如图,在△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为4,3,5,则 ( ) A.5=3sin B B.3=5sin B C.4=3tan B D.3=5tan B 2.如图所示的为一节楼梯的示意图,BC⊥AC,∠BAC=α,AC=6米.现要在楼梯上铺一块地毯,楼梯的宽度为1米,则地毯的面积至少需要 ( ) A.(+6)m2 B.(6tan α+6)m2 C. m2 D. m2 3.如图,在相邻两个山坡上,分别有垂直于水平面的通信基站MA和ND.甲在山脚点C处测得通信基站顶端M的仰角为60°,测得点C距离通信基站MA的水平距离CB为30 m;乙在另一座山脚点F处测得点F距离通信基站ND的水平距离FE为50 m,测得山坡DF的坡度i=1∶1.25.若ND=DE,点C,B,E,F在同一水平线上,则两个通信基站的顶端M与顶端N的高度差为(参考数据:≈1.41,≈1.73) ( ) A.9.0 m B.12.8 m C.13.1 m D.22.7 m 4.已知在锐角△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,有以下结论:===2R(其中R为△ABC的外接圆半径)成立.在△ABC中,若∠A=75°,∠B=45°,c=4,则△ABC的外接圆面积为 ( ) A. B. C.16π D.64π 5.小明使用测角仪在甲楼底端A处测得塔顶C处的仰角为53°,在甲楼B处测得塔顶C处的仰角为45°,已知AB=4.5米,则塔顶C处距离地面AD的高度为 ( ) (参考数据:sin 53°≈0.80,cos 53°≈0.60,tan 53°≈1.33) A.13.6米 B.18.1米 C.17.3米 D.16.8米 6.如图,在正方形网格中,每个小正方形的边长均为1,线段AC和BD的端点都在网格线的交点上.若AC与BD相交于点E,则tan∠AEB的值为 ( ) A. B. C. D.2 二、填空题(本题共4小题,每小题5分,共20分) 7.平放在地面上的三角形铁板ABC的一部分被沙堆掩埋,其示意图如图所示,量得∠A为54°,∠B为36°,边AB的长为2.1 m,BC边上露出部分BD的长为0.6 m,则铁板BC边被掩埋部分CD的长是 m.(结果精确到0.1 m.参考数据:sin 54°≈0.81,cos 54°≈0.59,tan 54°≈1.38) 8.如图,在△ABC中,∠C=90°,D是AC边上一点,且AD=BD=5,tan∠CBD=,线段AB的长度是 . 9.如图1所示的是一辆高空作业升降车的工作实景图,图2是其工作示意图,AC是可以伸缩的起重臂,其转动点A离地面BD的高度AH为1.6 m.当起重臂AC的长度为18 m,张角∠HAC为130°时,则操作平台C离地面的高度为 m.(结果精确到0.1 m,参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84) 10.如图,在一个坡比为1∶,坡长为20米的小山坡上生长着一棵树(CD).身高1.8米的小明(AB)在山坡上走了12米后抬头看到树的顶端,仰角为45°,则树的高度有 米. 三、解答题(本大题共5小题,共50分) 11.(8分)求下列各式的值: (1)2sin 30°+3cos 60°-4tan 45°; (2)tan 60°-+2cos 30°+1. 12.(10分)如图①,将“欢迎光临”门挂倾斜放置时,测得挂绳的一段AC=30 cm,另一段BC=20 cm.已知两个固定扣之间的距离AB=30 cm. (1)求点C到AB的距离; (2)如图②,将该门挂扶“正”(即AC=BC),求∠CAB的度数. (参考数据:sin 49°≈0.75,cos 41°≈0.75,tan 37°≈0.75,cos 53°≈0.6,tan 53°≈) 13.(10分)已知:如图,在Rt△ABC中,∠C=90°,AB的垂直平分线与AB,BC分别交于点E和点D,且BD=2AC. (1)求∠B的度数; (2)求tan∠BAC的值.(结果保留根号) 14.(10分)在数学综合实践活动课上,某小组要测量学校升旗台旗杆的高度.如图所示,测得BC∥AD,斜坡AB的长为6 m,坡度i=1∶,在点B处测得旗杆顶端E的仰角为70°,点B到旗杆底端C的距离为5 m. (1)求斜坡AB的坡角α的度数. (2)求旗杆顶端离地面的高度ED.(参考数据:sin 70°≈0.94,cos 70°≈0.34,tan 70°≈2.75,结果精确到1 m) 15.(12分)性质探究 如图1,在等腰三角形ABC中,∠ACB=120°,则底边AB与腰AC的长度之比为 . 理解运用 如图2,在四边形EFGH中,EF=EG=EH ... ...
~~ 您好,已阅读到文档的结尾了 ~~

