专项训练卷（一）反比例函数与一次函数或几何图形的结合（含答案） 2024-2025北师大版九年级数学上册

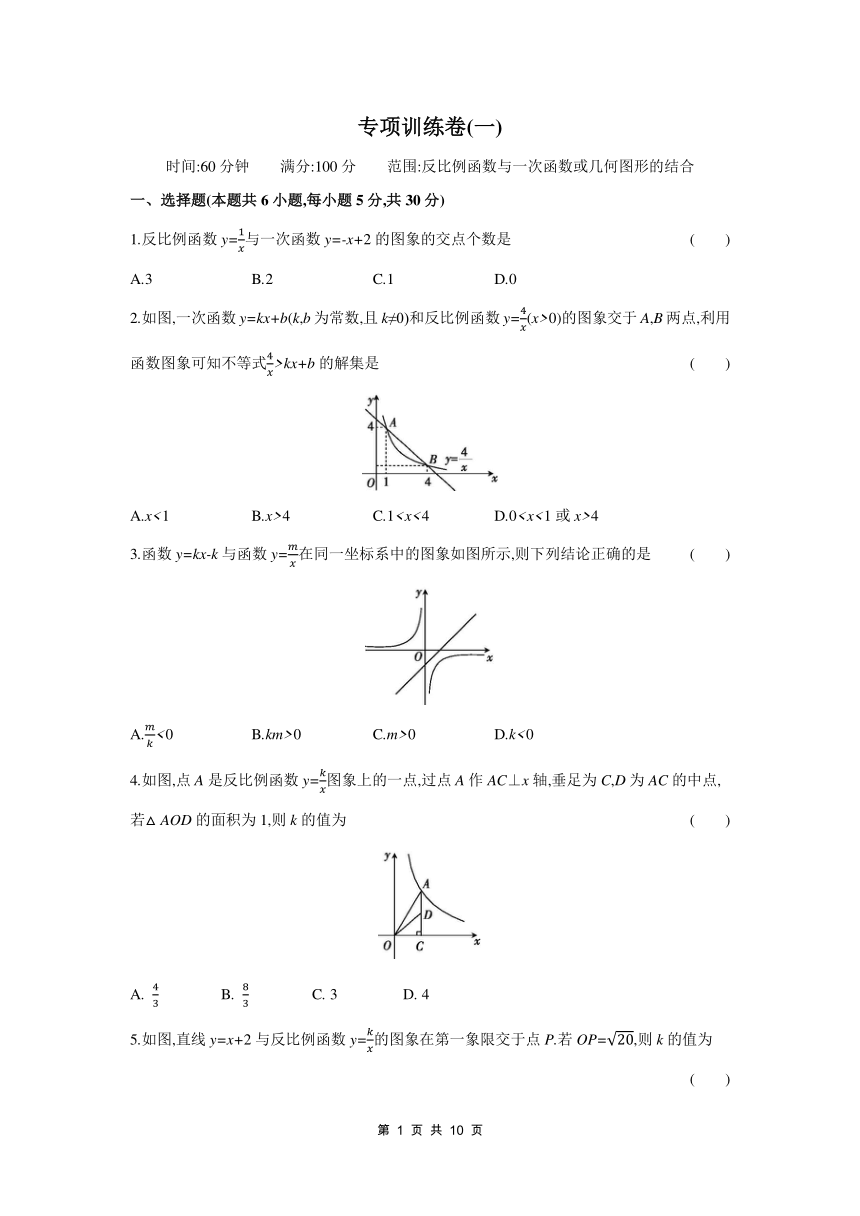
专项训练卷(一) 时间:60分钟　　满分:100分　　范围:反比例函数与一次函数或几何图形的结合 一、选择题(本题共6小题,每小题5分,共30分) 1.反比例函数y=与一次函数y=-x+2的图象的交点个数是 (　　) A.3 B.2 C.1 D.0 2.如图,一次函数y=kx+b(k,b为常数,且k≠0)和反比例函数y=(x>0)的图象交于A,B两点,利用函数图象可知不等式>kx+b的解集是 (　　) A.x<1 B.x>4 C.14 3.函数y=kx-k与函数y=在同一坐标系中的图象如图所示,则下列结论正确的是 (　　) A.<0 B.km>0 C.m>0 D.k<0 4.如图,点A是反比例函数y=图象上的一点,过点A作AC⊥x轴,垂足为C,D为AC的中点,若△AOD的面积为1,则k的值为 (　　) A. B. C. 3 D. 4 5.如图,直线y=x+2与反比例函数y=的图象在第一象限交于点P.若OP=,则k的值为 (　　) A.6 B.8 C.10 D.12 6.小浩通过学习物理了解到“区间测速”的知识:利用雷达、摄像头等现代手段记录汽车进出区间路段所用的时间,再根据区间路段的长度计算出汽车在该路段的平均速度(如图1).小浩将知识与生活实际相结合,给出了一个区间测速路段的函数图象(如图2),发现汽车速度v km/h与行驶时间t h是反比例函数关系.若该区间路段限速120 km/h,则行驶时间t应该 (　　) A.小于0.2 h B.小于0.5 h C.不小于0.5 h D.不小于0.2 h 二、填空题(本题共4小题,每小题5分,共20分) 7.如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=(m≠0)的图象交于点A(-1,2),B(2,-1),则不等式kx+b<的解集是　　　　. 8.如图,矩形ABCD的边AB与y轴平行,顶点A,C的坐标为(1,m),(3,m+6),那么同时经过点B与点D的反比例函数图象的表达式为　　　　. 9.如图,反比例函数y=(x>0)的图象经过A,B两点,过点A作AC⊥y轴于点C,过点B作BD⊥y轴于点D,过点B作BE⊥x轴于点E,连接AD,已知AC=1,BE=1,S矩形BEOD=4,则S△ACD=　　　　. 10.如图,正比例函数y=x与反比例函数y=(x>0)的图象交于点A,过点A作AB⊥y轴于点B,点C在线段AB上,且AC=OC.点P为y轴上一动点,当△POC与△PAC的面积相等时,点P的坐标为　　　　. 三、解答题(本大题共5小题,共50分) 11.(8分)如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=(m≠0)的图象相交于点A(1,2),B(a,-1). (1)求反比例函数和一次函数的解析式. (2)若直线y=kx+b(k≠0)与x轴交于点C,x轴上是否存在一点P,使S△APC=4 若存在,请求出点P坐标;若不存在,说明理由. 12.(10分)如图,在平面直角坐标系中,直线y=-nx+12(n≠0)与坐标轴的正半轴相交于A,B两点,与反比例函数y=的图象相交于第一象限内的C,D两点,点C,D是线段AB的三等分点. (1)用含n的代数式表示点B的坐标; (2)若n=2,求反比例函数y=的解析式. 13.(10分)如图,在平面直角坐标系中,点M为OA的中点,AB⊥x轴于点B,反比例函数y=(k>0,x>0)的图象经过点M,交AB于点C. (1)若点A的坐标为(2,6),则k=　　　　,点C的坐标为　　　　; (2)连接MC,OC,若△OMC的面积为3,求k的值. 14.(10分)如图,经过原点O的直线与反比例函数y=(a>0)的图象交于A,D两点(点A在第一象限),点B,C,E在反比例函数y=(b<0)的图象上,AB∥y轴,AE∥CD∥x轴,五边形ABCDE的面积为56,四边形ABCD的面积为32.求下列各式的值: (1)a-b; (2). 15.(12分)如图,在平面直角坐标系xOy中,△OA1B1是等边三角形,点B1的坐标是(2,0),反比例函数y=的图象经过点A1. (1)求反比例函数的解析式. (2)如图,以B1为顶点作等边三角形B1A2B2,使点B2在x轴上,点A2在反比例函数y=的图象上.若要使点B2在反比例函数y=的图象上,需将△B1A2B2向上平移多少个单位长度 参考答案 一、选择题 1 2 3 4 5 6 C D A D B D 4. D　【解析】∵AC⊥x轴,∴S△AOC=OC·AC=|k|.∵点D是AC的中点,S△AOD=1,∴S△AOC=2S△AOD=2,∴|k|=2,即|k|=4,∵k>0,∴k=4. 5.B　【解析】设点P(m,m+2),∵OP=,∴=,解得m1=2,m2=-4(不合题 ... ...