2025年九年级中考数学三轮冲刺训练几何图形中点问题训练（含解析）

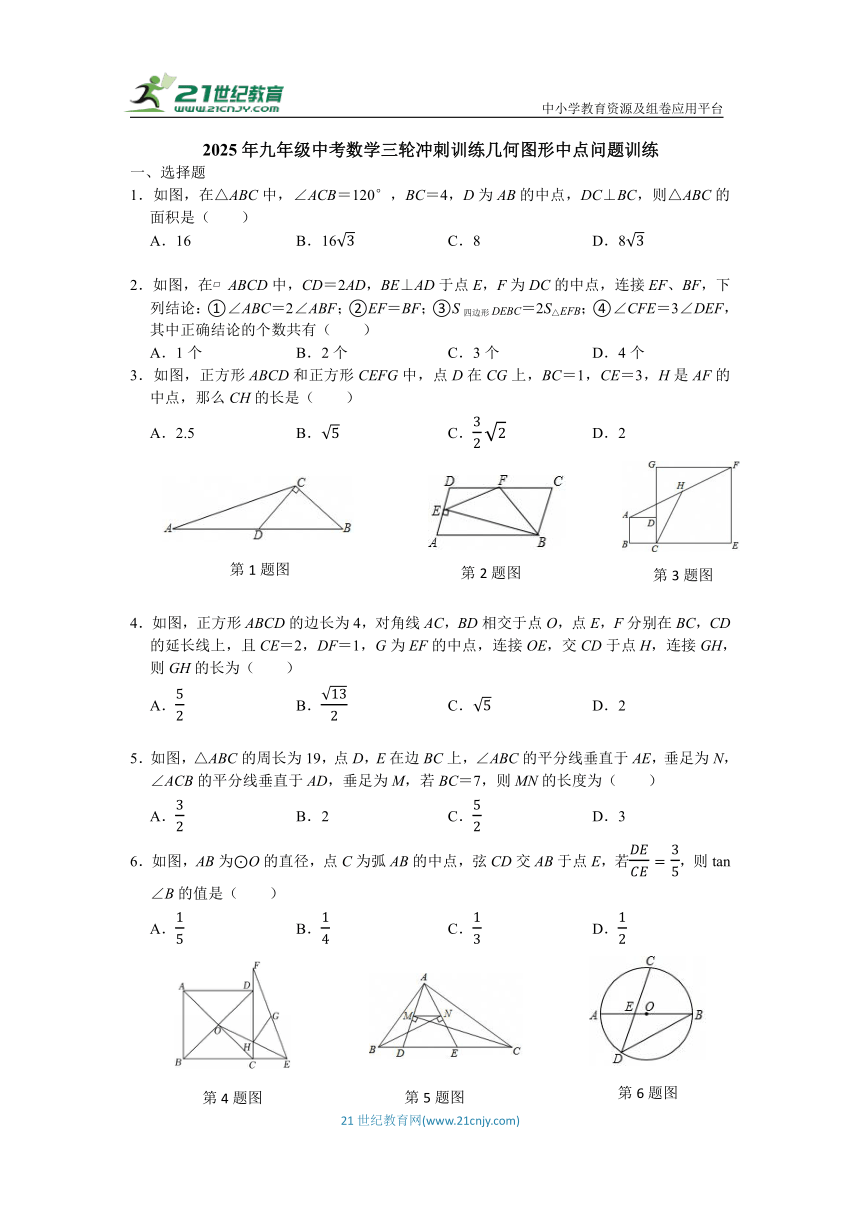
中小学教育资源及组卷应用平台 2025年九年级中考数学三轮冲刺训练几何图形中点问题训练 一、选择题 1．如图，在△ABC中，∠ACB＝120°，BC＝4，D为AB的中点，DC⊥BC，则△ABC的面积是（　　） A．16 B．16 C．8 D．8 2．如图，在 ABCD中，CD＝2AD，BE⊥AD于点E，F为DC的中点，连接EF、BF，下列结论：①∠ABC＝2∠ABF；②EF＝BF；③S四边形DEBC＝2S△EFB；④∠CFE＝3∠DEF，其中正确结论的个数共有（　　） A．1个 B．2个 C．3个 D．4个 3．如图，正方形ABCD和正方形CEFG中，点D在CG上，BC＝1，CE＝3，H是AF的中点，那么CH的长是（　　） A．2.5 B． C． D．2 4．如图，正方形ABCD的边长为4，对角线AC，BD相交于点O，点E，F分别在BC，CD的延长线上，且CE＝2，DF＝1，G为EF的中点，连接OE，交CD于点H，连接GH，则GH的长为（　　） A． B． C． D．2 5．如图，△ABC的周长为19，点D，E在边BC上，∠ABC的平分线垂直于AE，垂足为N，∠ACB的平分线垂直于AD，垂足为M，若BC＝7，则MN的长度为（　　） A． B．2 C． D．3 6．如图，AB为⊙O的直径，点C为弧AB的中点，弦CD交AB于点E，若，则tan∠B的值是（　　） A． B． C． D． 二、填空题 7．如图，在边长为2的等边三角形ABC中，D，E分别为AB，BC的中点，EF⊥AC于点F，G为EF的中点，连接DG，则DG的长为 　 　 ． 8．如图，DE是△ABC的中位线，F为DE中点，连接AF并延长交BC于点G，若S△EFG＝1，则S△ABC＝　 　 ． 9．如图，矩形ABCD中，AB＝4，AD＝2，E为AB的中点，F为EC上一动点，P为DF中点，连接PB，则PB的最小值是 　 　 ． 10．如图，在Rt△ABC中，∠ACB＝90°，D是AB的中点，连接CD，过点B作CD的垂线，交CD延长线于点E．AC＝30，，则cos∠DBE＝　 　 ． 11．如图，AB、CD是⊙O的直径，P为上一个动点（不与B、C重合），PM、PN分别垂直CD、AB，垂足分别为点M、N．若∠AOC＝60°，OA＝4，则MN的长为　 　 ． 三、解答题 12．如图，在△ABC中，AE平分∠BAC，BE⊥AE于点E，点F是BC的中点． （1）如图1，BE的延长线与AC边相交于点D，求证：EF（AC﹣AB）； （2）如图2，写出线段AB、AC、EF的数量关系，并证明你的结论． 13．如图所示，在△ABC中，AD是边BC上的高线，CE是边AB上的中线，DG⊥CE于点G，CD＝AE． （1）证明：CG＝EG． （2）若AB＝10，AD＝6，求CE的长． 14．如图，四边形ABCD中，∠BAD＝90°，∠DCB＝90°，E、F分别是BD、AC的中点， （1）请你猜测EF与AC的位置关系，并给予证明； （2）当AC＝8，BD＝10时，求EF的长． 15．如图，AB为⊙O的直径，半径OD⊥AB，⊙O的切线CE交AB的延长线于点E，⊙O的弦CD与AB相交于点F． （1）求证：EF＝EC； （2）若OE＝10，且B为EF的中点，求⊙O的半径长． 16．如图，半圆⊙O中，直径AB＝4，点C为弧AB的中点，点D在弧BC上，连结CD并延长交AB的延长线于点E，连结AD交CO于点F，连结EF． （1）求证：△DCA∽△ACE． （2）若点D为CE中点，求BE的长． （3）①△ACE面积与△AEF面积的差是定值吗？如果是，请求出该定值；若不是，请说明理由； ②若tan∠AEF，求AF的长． 17．已知直角△ABC，∠BAC＝90°，D是斜边BC的中点，E、F分别是AB、AC边上的点，且DE⊥DF，连接EF． （1）如图1，求证：∠BED＝∠AFD； （2）如图1，求证：BE2+CF2＝EF2； （3）如图2，当∠ABC＝45°，若BE＝4，CF＝3，求△DEF的面积． 18．如图，在△ABC中，∠BAC＝90°，AB＝AC＝12，点P在边AB上，D、E分别为BC、PC的中点，连接DE．过点E作BC的垂线，与BC、AC分别交于F、G两点，连接DG，交PC于点H． （1）∠EDC的度数为 　 　 °； （2）PE与DG存在怎样的位置关系与数量关系？请说明理由； （3）连接PG，求△APG的面积的最大值． 19．如图，在△ABC中，AD平分∠BAC交BC边于点D ... ...