2025届高二下学期数学期中综合模拟试题（人教A ）（二）

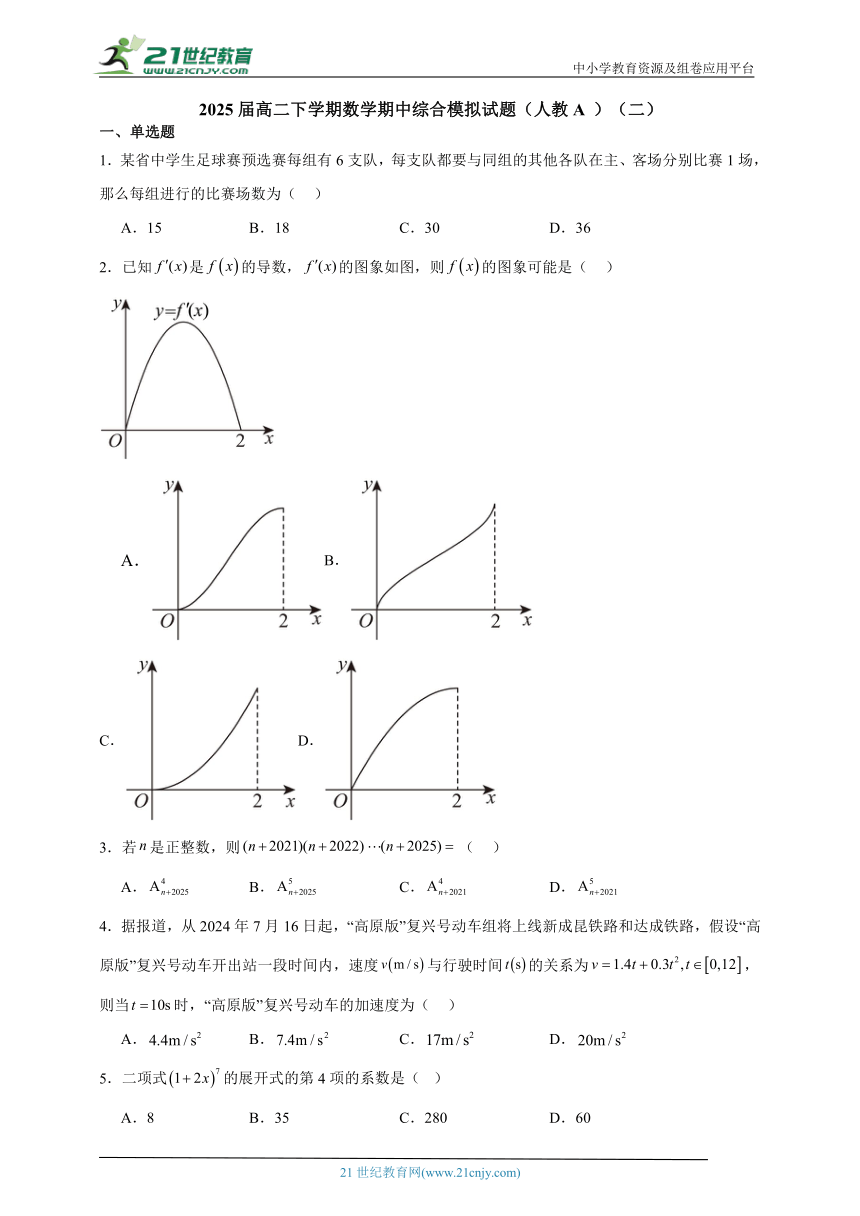
中小学教育资源及组卷应用平台 2025届高二下学期数学期中综合模拟试题（人教A ）（二） 一、单选题 1．某省中学生足球赛预选赛每组有6支队，每支队都要与同组的其他各队在主、客场分别比赛1场，那么每组进行的比赛场数为（ ） A．15 B．18 C．30 D．36 2．已知是的导数，的图象如图，则的图象可能是（ ） B． C．D． 3．若是正整数，则（ ） A． B． C． D． 4．据报道，从2024年7月16日起，“高原版”复兴号动车组将上线新成昆铁路和达成铁路，假设“高原版”复兴号动车开出站一段时间内，速度与行驶时间的关系为，则当时，“高原版”复兴号动车的加速度为（ ） A． B． C． D． 5．二项式的展开式的第4项的系数是（ ） A．8 B．35 C．280 D．60 6．最优化原理是指要求目前存在的多种可能的方案中，选出最合理的，达到事先规定的最优目标的方案，这类问题称之为最优化问题.为了解决实际生活中的最优化问题，我们常常需要在数学模型中求最大值或者最小值.下面是一个有关曲线与直线上点的距离的最值问题，请你利用所学知识来解答：若点是曲线上任意一点，则点到直线的距离的最小值为（ ） A． B． C． D． 7．将6本不同的书（包括1本物理书和1本历史书）平均分给甲、乙两人，其中物理书和历史书不能分给同一个人，则不同的分配种数是（ ） A．6 B．12 C．18 D．24 8．若函数是增函数，则的取值范围是（ ） A． B． C． D． 二、多选题 9．在的展开式中，则（ ） A．x的系数为135 B．第4项的二项式系数为10 C．无常数项 D．所有项的系数之和为125 10．口袋中装有6个白球和8个红球，每个球编有不同的号码，现从中取出2个球，下列说法正确的有（ ） A．恰好是白球、红球各一个的取法有48种 B．恰好是两个白球的取法有30种 C．至少有一个白球的取法有63种 D．两球的颜色相同的取法有43种 11．若存在，使得对任意恒成立，则函数在上有下界，其中为函数的一个下界；若存在，使得对任意恒成立，则函数在上有上界，其中为函数的一个上界.如果一个函数既有上界又有下界，那么称该函数有界.下列说法正确的是（ ） A．2是函数的一个下界 B．函数有下界，无上界 C．函数有上界，无下界 D．函数有界 三、填空题 12．在二项式的展开式中，所有二项式系数和为64，则常数项为 .（用数字作答） 13．的单调递减区间为 . 14．设一个四位数的个位数、十位数、百位数、千位数分别为a，b，c，d，当时，称这个四位数为“和对称四位数”，且为这个“和对称四位数”的对称和，例如8440是一个“和对称四位数”，其对称和为8，则对称和不大于4的“和对称四位数”的个数为 ． 四、解答题 15．（1）解不等式； （2）计算：；（结果用数字表示） 16．已知函数． (1)求函数的单调区间； (2)求函数在区间上的最大值与最小值． 17．已知的展开式的第2项与第3项的二项式系数之比是. (1)求的值； (2)求展开式的常数项； (3)求展开式中系数绝对值最大的项. 18．记、分别为函数、的导函数．若存在，满足且，则称为函数与的一个“点”． （1）证明：函数与不存在“点”； （2）若函数与存在“点”，求实数的值． 19．已知函数（为常数）. (1)求证：当时，； (2)讨论函数的单调性； (3)不等式在上恒成立，求实数的最小整数值. 参考答案 1．C 根据分步乘法计数原理进行计算即可. 可以先从这6支队中选1支为主队，然后从剩下的5支队中选1支为客队. 按分步乘法计数原理，每组进行的比赛场数为. 故选：C. 2．A 利用导函数的正负及变化规律即可判断. 由的图象可知，，所以的图象单调递增， 因为的值先增大后减小，所以的切线的斜率先增大后减小，根据图象可判断A正确. 故选：A. 3．B 根据排列数公式，即可确定目标乘式对应的排列数. 由，且都为正整数， 故． 故选：B 4．B 根 ... ...