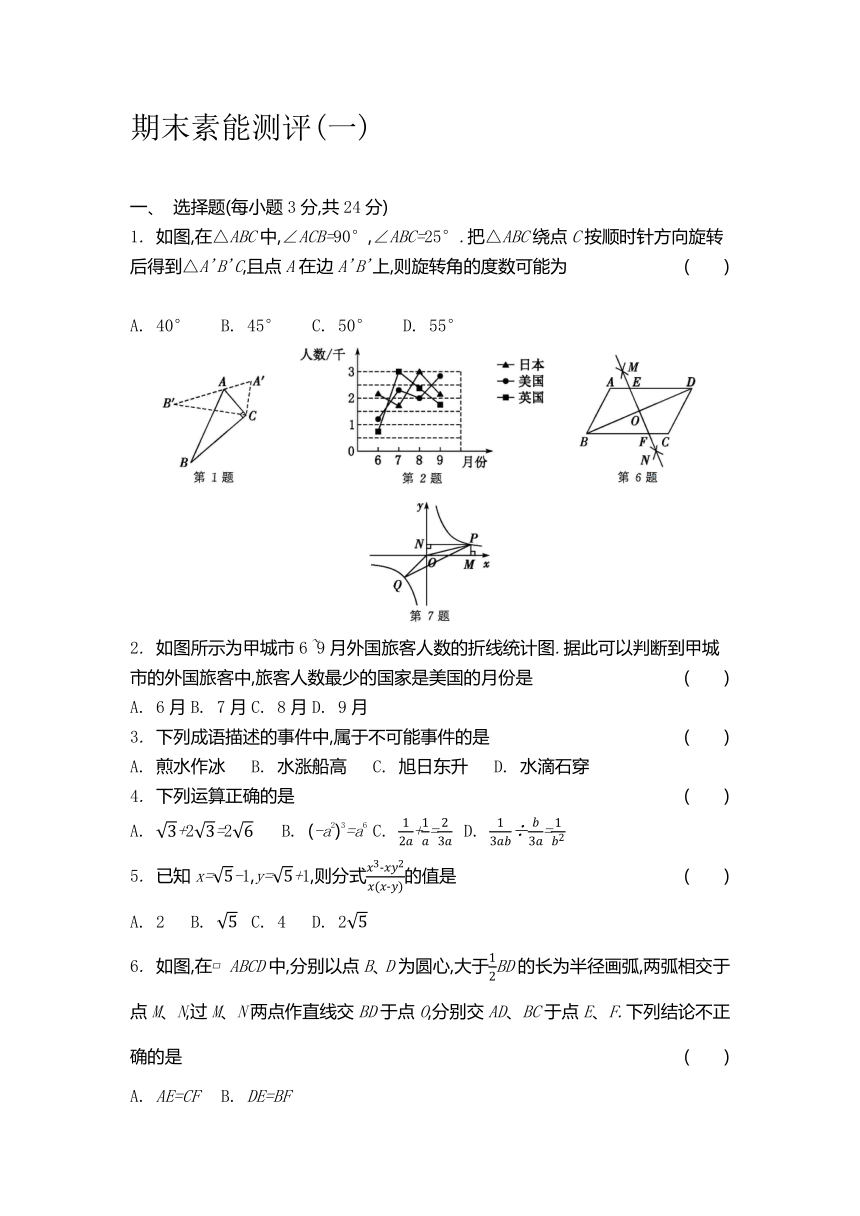
期末素能测评(一) 一、 选择题(每小题3分,共24分) 1. 如图,在△ABC中,∠ACB=90°,∠ABC=25°.把△ABC绕点C按顺时针方向旋转后得到△A'B'C,且点A在边A'B'上,则旋转角的度数可能为 ( ) A. 40° B. 45° C. 50° D. 55° 2. 如图所示为甲城市6~9月外国旅客人数的折线统计图.据此可以判断到甲城市的外国旅客中,旅客人数最少的国家是美国的月份是 ( ) A. 6月 B. 7月 C. 8月 D. 9月 3. 下列成语描述的事件中,属于不可能事件的是 ( ) A. 煎水作冰 B. 水涨船高 C. 旭日东升 D. 水滴石穿 4. 下列运算正确的是 ( ) A. +2=2 B. (-a2)3=a6 C. += D. ÷= 5. 已知x=-1,y=+1,则分式的值是 ( ) A. 2 B. C. 4 D. 2 6. 如图,在 ABCD中,分别以点B、D为圆心,大于BD的长为半径画弧,两弧相交于点M、N,过M、N两点作直线交BD于点O,分别交AD、BC于点E、F.下列结论不正确的是 ( ) A. AE=CF B. DE=BF C. OE=OF D. DE=DC 7. 如图,点P(m,1)、Q(-2,n)都在反比例函数y=的图像上.过点P分别向x轴、y轴作垂线,垂足分别为M、N,连接OP、OQ、PQ.若四边形OMPN的面积记作S1,△POQ的面积记作S2,则 ( ) A. S1∶S2=2∶3 B. S1∶S2=1∶1 C. S1∶S2=4∶3 D. S1∶S2=5∶3 8. 菱形ABCD的边长为2,∠A=60°,将该菱形绕顶点A在平面内旋转30°,则旋转后的图形与原图形重叠部分的面积为 ( ) A. 3- B. 2- C. -1 D. 2-2 二、 填空题(每小题3分,共24分) 9. 如图,在平面直角坐标系中有两点A(3,3)、B(3,1),反比例函数y=图像的一支与线段AB有交点,写出一个符合条件的k的整数值: . 10. 当x=-2时,分式无意义;当x=4时,此分式的值为0,则a+b的值为 . 11. 计算+的结果为 . 12. 如图,在△ABC中,M、N分别是AB和AC的中点,连接MN,E是CN的中点,连接ME并延长,交BC的延长线于点D.若BC=4,则CD的长为 . 13. 若关于x的方程-3=的解为非负数,则m的取值范围是 . 14. 在平面直角坐标系中,函数y=(x>0)与y=x-1的图像交于点P(a,b),则代数式-的值为 . 15. 如图,菱形ABCD的边长为2,∠ABC=60°,对角线AC与BD交于点O,E为OB的中点,F为AD的中点,连接EF,则EF的长为 . 16. 将邻边长分别为、1的矩形纸片剪成四个等腰三角形纸片(无剩余纸片).有下列数:① ;② 1;③ -1;④ ;⑤ .其中,可以作为一个等腰三角形的腰长的是 (填序号). 三、 解答题(共82分) 17. (5分)计算: (1) ÷; (2) |-|+-. 18. (5分)解方程: (1) -=1; (2) -=1. 19. (6分)某校对九年级学生进行一次综合文科中考模拟测试,根据成绩x(单位:分,x为整数),评定为优秀、良好、合格、不合格四个等级(优秀、良好、合格、不合格分别用A、B、C、D表示),A等级:90≤x≤100,B等级:80≤x<90,C等级:60≤x<80,D等级:0≤x<60.该校随机抽取了一部分学生的成绩进行调查,并绘制成不完整的统计表和如图所示的不完整的频数分布直方图. 等 级 频 数 频 率 A a 20% B 16 40% C b m D 4 10% 请根据给出的信息,解答下列问题: (1) 统计表中,a= ,b= ,m= . (2) 本次调查共抽取了多少名学生 请补全频数分布直方图. (3) 若该校九年级有800名学生,请估计成绩为优秀的学生有多少名. 20. (6分)已知反比例函数y=的图像分别位于第二、四象限,化简:-+. 21. (6分)王老师将8个黑球和若干个红球放入一个不透明的袋子中并搅匀,让若干学生进行摸球试验,每次摸出1个球并记下颜色(有放回),不断重复,试验中的一组统计数据如下表: 摸球的次数n 100 150 200 500 800 1000 摸出红球的次数m 59 93 118 290 480 601 摸出红球的频率 0.59 0.59 0.60 0.601 (1) 将表格补充完整; (2) 摸出红球的概率的估计值是 (精确到0.1); (3) 估计袋子 ... ...
~~ 您好,已阅读到文档的结尾了 ~~