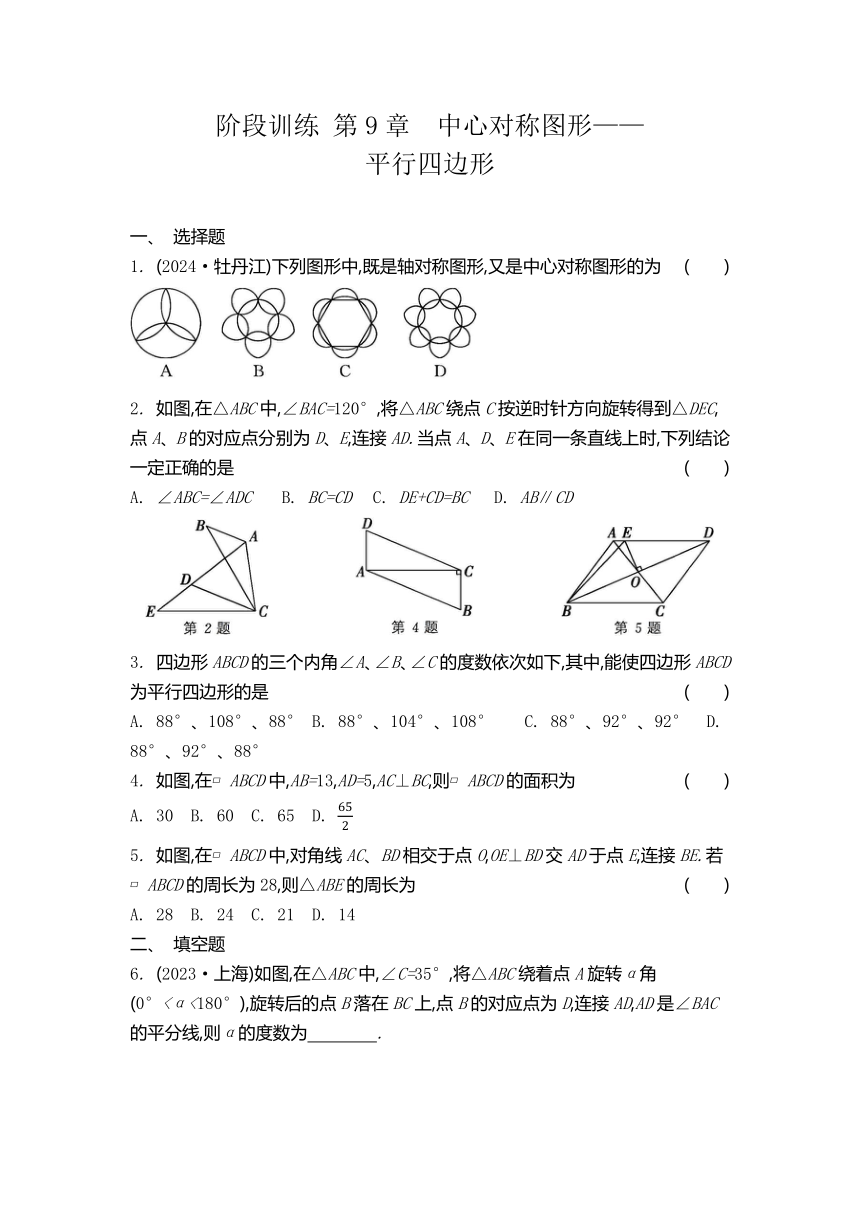
阶段训练 第9章 中心对称图形——— 平行四边形 一、 选择题 1. (2024·牡丹江)下列图形中,既是轴对称图形,又是中心对称图形的为 ( ) 2. 如图,在△ABC中,∠BAC=120°,将△ABC绕点C按逆时针方向旋转得到△DEC,点A、B的对应点分别为D、E,连接AD.当点A、D、E在同一条直线上时,下列结论一定正确的是 ( ) A. ∠ABC=∠ADC B. BC=CD C. DE+CD=BC D. AB∥CD 3. 四边形ABCD的三个内角∠A、∠B、∠C的度数依次如下,其中,能使四边形ABCD为平行四边形的是 ( ) A. 88°、108°、88° B. 88°、104°、108° C. 88°、92°、92° D. 88°、92°、88° 4. 如图,在 ABCD中,AB=13,AD=5,AC⊥BC,则 ABCD的面积为 ( ) A. 30 B. 60 C. 65 D. 5. 如图,在 ABCD中,对角线AC、BD相交于点O,OE⊥BD交AD于点E,连接BE.若 ABCD的周长为28,则△ABE的周长为 ( ) A. 28 B. 24 C. 21 D. 14 二、 填空题 6. (2023·上海)如图,在△ABC中,∠C=35°,将△ABC绕着点A旋转α角(0°<α<180°),旋转后的点B落在BC上,点B的对应点为D,连接AD,AD是∠BAC的平分线,则α的度数为 . 7. 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,将△ABC绕点C按逆时针方向旋转到△EDC的位置,连接AE.若CD⊥AB,则∠CAE的度数为 . 8. 如图,F是△ABC内的一点,FD∥BC,FE∥AB.若 BDFE的面积为2,BD=BA,BE=BC,则△ABC的面积是 . 9. 如图,在 ABCD中,DF平分∠ADC,交AB于点F,BE∥DF,交AD的延长线于点E.若∠A=40°,则∠ABE的度数为 . 10. 如图, ABCD的顶点C在等边三角形BEF的边BF上,点E在AB的延长线上,G为DE的中点,连接CG.若AD=3,AB=CF=2,则CG的长为 . 11. (2023·泰州)如图,在△ABC中,AB=AC,∠A=30°,射线CP从射线CA开始绕点C按逆时针方向旋转α角(0°<α<75°),与射线AB相交于点D,将△ACD沿射线CP翻折至△A'CD处,射线CA'与射线AB相交于点E.若△A'DE是等腰三角形,则α的度数为 . 三、 解答题 12. 如图,在△AFC中,∠FAC=45°,FE⊥AC于点E,在EF上取一点B,连接AB、BC,使得AB=FC,过点A作AD⊥AF,且AD=BC,连接CD.求证:四边形ABCD是平行四边形. 第12题 13. 如图,在△ABC中,点E在边BC上,AE=AB,将线段AC绕点A旋转到AF的位置,使得∠CAF=∠BAE,连接EF,EF与AC交于点G. (1) 求证:BC=EF; (2) 若∠ABC=65°,∠ACB=28°,求∠FGC的度数. 第13题 一、 1. C 2. D 3. D 4. B 5. D 二、 6. ° 7. 75° 8. 12 9. 70° 10. 解析:延长CG交BE于点H.先证明△DCG≌△EHG,得CD=HE=2,CG=HG.再证明△BCH为等边三角形,得CH=BC=AD=3,从而CG=CH=. 11. 22.5°或67.5°或45° 解析:分三种情况分别进行计算:① 当A'D=A'E时;② 当DA'=DE时;③ 当ED=EA'时. 三、 12. ∵ FE⊥AC,∴ ∠FEA=∠FEC=90°.∵ ∠FAC=45°,∴ ∠FAE=∠AFE=45°.∴ AE=FE.在Rt△AEB和Rt△FEC中,∴ Rt△AEB≌Rt△FEC.∴ BE=CE.∴ ∠CBE=∠BCE=45°.∵ AD⊥AF,∴ ∠FAD=90°.∴ ∠CAD=∠FAD-∠FAC=90°-45°=45°.∴ ∠BCE=∠CAD.∴ AD∥BC.又∵ AD=BC,∴ 四边形ABCD是平行四边形 13. (1) ∵ ∠CAF=∠BAE,∴ ∠BAE+∠EAC=∠CAF+∠EAC,即∠BAC=∠EAF.∵ 将线段AC绕点A旋转到AF的位置,∴ AC=AF.在△ABC和△AEF中,∴ △ABC≌△AEF.∴ BC=EF (2) ∵ AB=AE,∴ ∠AEB=∠ABC=65°.∴ ∠BAE=180°-65°×2=50°.∴ ∠FAG=∠BAE=50°.∵ △ABC≌△AEF,∴ ∠F=∠C=28°.∴ ∠FGC=∠FAG+∠F=50°+28°=78° ... ...
~~ 您好,已阅读到文档的结尾了 ~~