2025年九年级中考数学三轮冲刺训练高频考点突破圆的切线的证明（含解析）

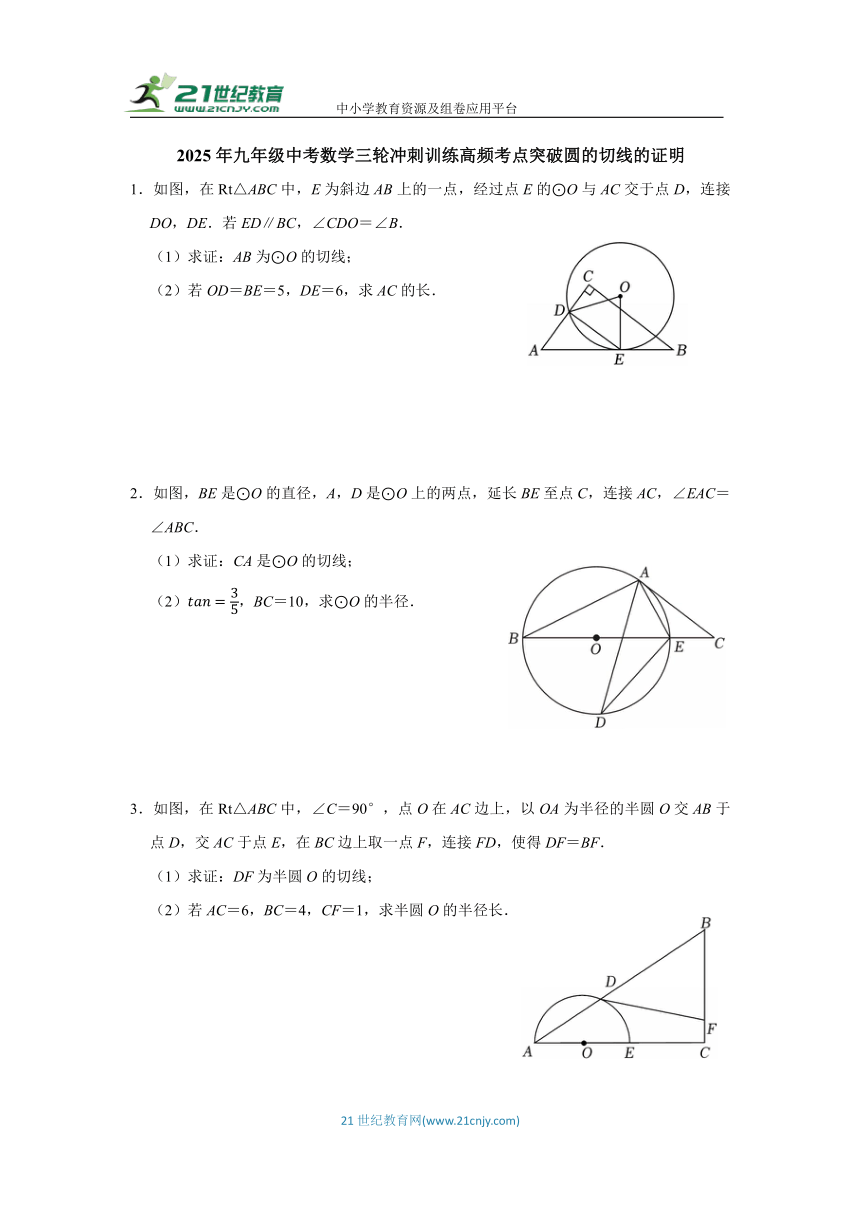
中小学教育资源及组卷应用平台 2025年九年级中考数学三轮冲刺训练高频考点突破圆的切线的证明 1．如图，在Rt△ABC中，E为斜边AB上的一点，经过点E的⊙O与AC交于点D，连接DO，DE．若ED∥BC，∠CDO＝∠B． （1）求证：AB为⊙O的切线； （2）若OD＝BE＝5，DE＝6，求AC的长． 2．如图，BE是⊙O的直径，A，D是⊙O上的两点，延长BE至点C，连接AC，∠EAC＝∠ABC． （1）求证：CA是⊙O的切线； （2），BC＝10，求⊙O的半径． 3．如图，在Rt△ABC中，∠C＝90°，点O在AC边上，以OA为半径的半圆O交AB于点D，交AC于点E，在BC边上取一点F，连接FD，使得DF＝BF． （1）求证：DF为半圆O的切线； （2）若AC＝6，BC＝4，CF＝1，求半圆O的半径长． 4．如图，AB为⊙O的直径，AD与⊙O相交于点E，∠DAB的平分线交⊙O于点C，∠ADC＝90°，连DO、AC相交于点F． （1）求证：CD是⊙O的切线； （2）若，求cos∠DAB的值． 5．△ABC中，AB＝BC，点D为AC中点，过点D作DE⊥BC于点E，点O在ED的延长线上，以O为圆心，OD为半径的圆经过点A． （1）求证：AB是⊙O的切线； （2）若sin∠BAC＝0.6，DE＝1，求BC的长． 6．如图，PA切⊙O于点A，AB是⊙O的直径，C是⊙O上一点，PA＝PC＝AB，连接PO交AC于点D． （1）求证：PC是⊙O的切线； （2）若BC＝2，求AB的长． 7．如图，AB为⊙O的直径，过圆上一点D作⊙O的切线CD交BA的延长线于点C，过点O作OE∥AD交CD于点E，连接BE． （1）求证：直线BE是⊙O的切线； （2）若CA＝2，CD＝4，求DE的长． 8．如图，AB为⊙O的直径，点C在⊙O上，∠ACB的平分线CD交⊙O于点D，过点D作DE∥AB，交CB的延长线于点E． （1）求证：DE是⊙O的切线； （2）若AC＝8，BC＝6，求AD及BE的长． 9．如图，△ABC中，以AB为直径的⊙O交BC于点E，AE平分∠BAC，过点E作ED⊥AC于点D，延长DE交AB的延长线于点P． （1）求证：PE是⊙O的切线； （2）若，BP＝4，求CD的长． 10．如图，AB为⊙O的直径，C、F为⊙O上两点，且点C为弧BF的中点，过点C作AF的垂线，交AF的延长线于点E，交AB的延长线于点D． （1）求证：DE是⊙O的切线； （2）若AE＝3，DE＝4，求⊙O的半径的长． 11．如图，AB是⊙O的直径，PB⊥AB，过点B作BC⊥OP交⊙O于点C，垂足为D，连接PC并延长与BA的延长线交于点M． （1）求证：PM是⊙O的切线； （2）若OD＝2，OP＝18，求的值． 12．如图，AB是⊙O的直径，点D是⊙O上一点，过点A的切线与弦BD的延长线交于点C，过点D的直线交线段AC于点E，且DE＝CE． （1）求证：直线DE与⊙O相切； （2）已知⊙O的半径是4，∠B＝30°，求阴影部分的面积． 13．如图⊙O是△ABC的外接圆，点O在BC上，∠BAC的角平分线交⊙O于点D，连接BD，CD，过点D作BC的平行线与AC的延长线相交于点P． （1）求证：PD是⊙O的切线； （2）若AB＝6，AC＝8，求DC与PC的值． 14．如图，在⊙O中，AB是直径，CD是弦，且AB⊥CD，垂足为E，AB＝20，CD＝12，在BA的延长线上取一点F，连接CF，使∠FCD＝2∠B． （1）求证：CF是⊙O的切线； （2）求EF的长． 15．如图，点C在以AB为直径的⊙O上，点D在BA的延长线上，∠DCA＝∠CBA． （1）求证：DC是⊙O的切线； （2）点G是半径OB上的点，过点G作OB的垂线与BC交于点F，与DC的延长线交于点E，若sinD，DA＝FG＝2，求CE的长． 16．如图，在Rt△ABC中，∠ACB＝90°，点E在AC上，以CE为直径的⊙O经过AB上的点D，与OB交于点F，且BD＝BC． （1）求证：AB是⊙O的切线； （2）若AD，AE＝1，求的长． 参考答案 1．【解答】（1）证明：∵ED∥BC，∠C＝90°， ∴∠AED＝∠B，∠CDE＝90°， 又∵∠CDO＝∠B， ∴∠AED＝∠CDO， ∵OD＝OE， ∴∠OED＝∠ODE， ∴∠AED+∠OED＝∠CDO+∠ODE＝90°，即∠AEO＝90°， 又∵OE是半径； ∴AB为⊙O的切线； （2）解：由（1） ... ...