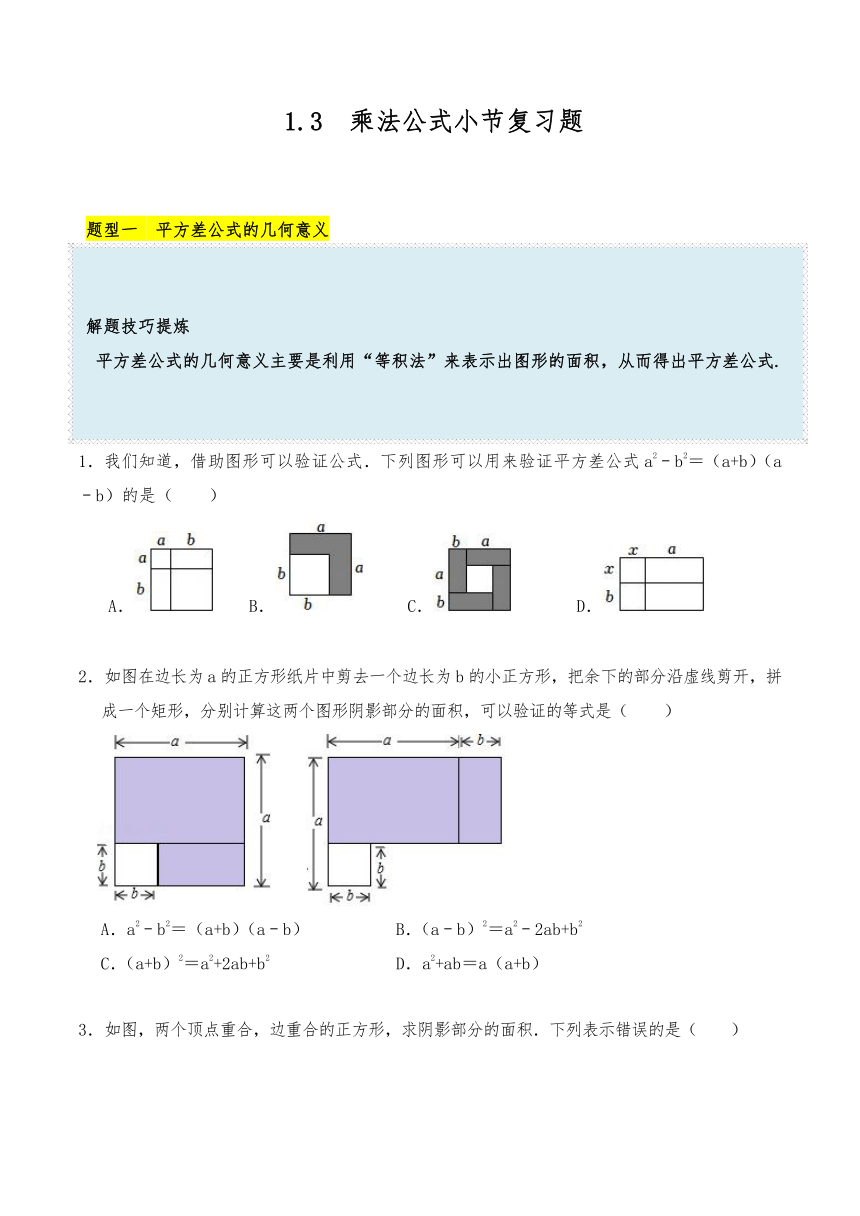
1.3 乘法公式小节复习题 题型一 平方差公式的几何意义 解题技巧提炼 平方差公式的几何意义主要是利用“等积法”来表示出图形的面积,从而得出平方差公式. 1.我们知道,借助图形可以验证公式.下列图形可以用来验证平方差公式a2﹣b2=(a+b)(a﹣b)的是( ) A. B. C. D. 2.如图在边长为a的正方形纸片中剪去一个边长为b的小正方形,把余下的部分沿虚线剪开,拼成一个矩形,分别计算这两个图形阴影部分的面积,可以验证的等式是( ) A.a2﹣b2=(a+b)(a﹣b) B.(a﹣b)2=a2﹣2ab+b2 C.(a+b)2=a2+2ab+b2 D.a2+ab=a(a+b) 3.如图,两个顶点重合,边重合的正方形,求阴影部分的面积.下列表示错误的是( ) A.a(a﹣b)+b2 B.a2﹣b2 C.(b+a)(a﹣b)×2 D.a(a﹣b)+b(a﹣b) 4.如图,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分沿虚线剪开,拼成右边的长方形,根据图形的变化过程写出正确的等式是( ) A.a2﹣b2=(a+b)(a﹣b) B.a2﹣ab=a(a﹣b) C.a2﹣b2=(a﹣b)2 D.a2﹣2ab+b2=(a﹣b)2 5.将图甲中阴影部分的小长方形变换到图乙位置,你能根据两个图形的面积关系得到的数学公式是( ) A.(a﹣b)(a+b)=a2﹣b2 B.(a+b)2=a2+2ab+b2 C.(a﹣b)2=a2﹣2ab+b2 D.(2a﹣b)2=4a2﹣4ab+b2 6.【探究】如图①,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分沿虚线剪开,拼成图②的长方形. (1)请你分别表示出这两个图形中阴影部分的面积:图① 图② ; (2)比较两图的阴影部分面积,可以得到乘法公式: (用字母a、b表示); 【应用】请应用这个公式完成下列各题: ①已知2m﹣n=3,2m+n=4,则4m2﹣n2的值为 12 ; ②计算:(x﹣3)(x+3)(x2+9); 【拓展】计算(2+1)(22+1)(24+1)(28+1)…(232+1)的结果为 . 题型二 直接利用平方差公式计算 解题技巧提炼 应用平方差公式计算时,应注意以下几个问题:(1) 左边是两个二项式相乘,并且这两个二项式中有一项完全相同,另一项互为相反数;(2) 右边是相同项的平方减去相反项的平方;(3) 公式中的 a 和 b 可以是具体的数,也可以是单项式或多项式. 1.在下列多项式乘法中,可以用平方差公式计算的是( ) A.(2a﹣3b)(﹣2a+3b) B.(﹣3a+4b)(﹣4b﹣3a) C.(a+1)(﹣a﹣1) D.(a2﹣b)(a+b2) 2.若(3b+a)( )=9b2﹣a2,则括号内应填的代数式是( ) A.﹣a﹣3b B.a+3b C.﹣3b+a D.3b﹣a 3.计算:(2a+b)(2a﹣b)=( ) A.4a2+b2 B.4a2﹣b2 C.2a2﹣b2 D.2a2+b2 4.在等式(﹣a﹣b)( )=a2﹣b2中,括号里应填的多项式是( ) A.﹣a+b B.a+b C.﹣a﹣b D.a﹣b 5.(﹣2x+3)(﹣2x﹣3)= . 6.若(x+y2)(x﹣y2)(x2+y4)=xm﹣yn,则m= ,n= . 7.计算: (1)(5ab﹣3x)(﹣3x﹣5ab) (2)(﹣y2+x)(x+y2) (3)x(x+5)﹣(x﹣3)(x+3) (4)(﹣1+a)(﹣1﹣a)(1+b2) 题型三 完全平方公式的几何意义 解题技巧提炼 平方差公式的几何意义主要是利用“等积法”来表示出图形的面积,从而得出完全平方公式. 1.如图,根据阴影部分面积和图形的面积关系可以得到的数学公式是( ) A.a(a+b)=a2+ab B.a(a﹣b)=a2﹣ab C.(a+b)2=a2+2ab+b2 D.(a﹣b)2=a2﹣2ab+b2 2.通过两种不同的方法计算同一图形的面积可以得到一个数学等式,用这种方法可得到整式乘法中的一些运算法则或公式,例如,由图1可得等式(a+b)(c+d)=ac+ad+bc+bd,即为多项式乘法法则.利用图2可得的乘法公式为( ) A.(a+b)2=a2+b2 B.(a+b)2=a2+2ab+b2 C.(a+b)2 ... ...
~~ 您好,已阅读到文档的结尾了 ~~