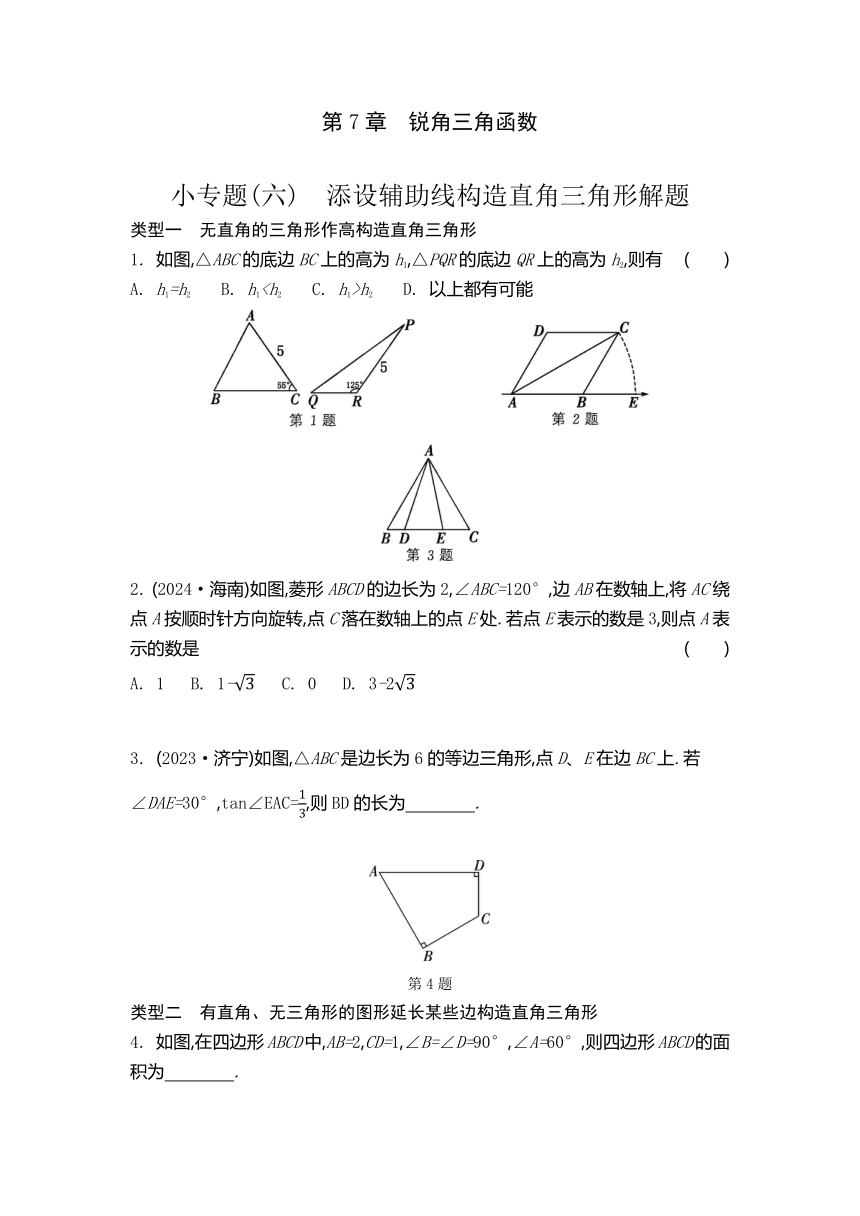
第7章 锐角三角函数 专题练习 （含答案）2024-2025学年数学苏科版九年级下册

第7章　锐角三角函数 小专题(六)　添设辅助线构造直角三角形解题 类型一　无直角的三角形作高构造直角三角形 1. 如图,△ABC的底边BC上的高为h1,△PQR的底边QR上的高为h2,则有 (　　) A. h1=h2 B. h1

h2 D. 以上都有可能 　　　　　　　　　　 2. (2024·海南)如图,菱形ABCD的边长为2,∠ABC=120°,边AB在数轴上,将AC绕点A按顺时针方向旋转,点C落在数轴上的点E处.若点E表示的数是3,则点A表示的数是 (　　) A. 1 B. 1- C. 0 D. 3-2 3. (2023·济宁)如图,△ABC是边长为6的等边三角形,点D、E在边BC上.若∠DAE=30°,tan∠EAC=,则BD的长为　　　　. 第4题 类型二　有直角、无三角形的图形延长某些边构造直角三角形 4. 如图,在四边形ABCD中,AB=2,CD=1,∠B=∠D=90°,∠A=60°,则四边形ABCD的面积为　　　　. 5. 如图,四边形ABCD内接于☉O,AB=17,CD=10,∠A=90°,cosB=,求AD的长. 第5题 类型三　有三角函数值,但不能直接利用时作垂线构造直角三角形 第6题 6. 如图,在△ABC中,∠ACB=90°,点D在AB的延长线上,连接CD.若AB=2BD,tan∠BCD=,则的值为　　　　. 7. 如图,在四边形ABCD中,对角线AC、BD交于点O,∠BCD是钝角,AB=AD,BD平分∠ABC.若CD=3,BD=2,sin∠DBC=,求AC的长. 第7题 类型四　求非直角三角形中角的三角函数值时构造直角三角形 8. 如图,C是以点O为圆心,AB为直径的半圆上一点,连接AC、BC、OC.若AC=4,BC=3,则sin∠BOC的值为 (　　) A. 1 B. C. D. 　　　　　　　　　　　　 9. 如图,在△ABC中,AB=AC=5,BC=8.若∠BPC=∠BAC,则tan∠BPC的值为　　　　. 10. 如图所示为由10个完全相同的正三角形构成的网格图,则cos(α+β)的值为　　　　. 11. 如图①,D为☉O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD. (1) 判断直线CD与☉O的位置关系,并说明理由; (2) 若tan∠CDA=,AC=2,求☉O的半径; (3) 如图②,在(2)的条件下,∠ADB的平分线DE交☉O于点E,交AB于点F,连接BE,则sin∠DBE的值为　　　　. 小专题(七)　圆中利用锐角三角函数解题的策略 类型一　利用圆周角的性质将角转化到直角三角形中 1. 　 如图,在☉O中,AB⊥OC,垂足为D,AB=8,CD=2.若P是优弧AB上的任意一点,则sin∠APB的值为 (　　) A. B. C. D. 　　　　　　　　 2. 如图,在4×4的正方形网格中,点A、B、C、D、O均在格点上,其中点A、B、D在☉O上,E是线段CD与☉O的交点,则∠BAE的正切值为　　　　. 3. (2024·济南)如图,AB、CD为☉O的直径,点E在上,连接AE、DE,点G在BD的延长线上,AB=AG,∠EAD+∠EDB=45°. (1) 求证:AG与☉O相切; (2) 若BG=4,sin∠DAE=,求DE的长. 第3题 类型二　利用直径所对的圆周角是直角构造直角三角形 4. (2023·威海)如图,在平面直角坐标系中,点P在第一象限内,☉P与x轴相切于点C,与y轴相交于点A(0,8)、B(0,2).连接AC、BC,则cos∠ACB的值为　　　　. 　　　　　　 5. 如图,P是☉O的直径AB的延长线上一点,过点P作直线交☉O于C、D两点.若OA=3,PB=2,则tan∠PAC·tan∠PAD的值为　　　　. 6. 如图,在△ABC中,AB=AC,以AB为直径的☉O交AC于点D,交BC于点E,直线EF⊥AC于点F,交AB的延长线于点H. (1) 求证:HF是☉O的切线; (2) 当EB=6,cos∠ABE=时,求tanH的值. 第6题 7. 如图,AD是☉O的直径,BD、BC都是弦,且BD=BC,经过点B作☉O的切线,交AD的延长线于点E. (1) 求证:∠EBD=∠CAB; (2) 若BC=,AC=5,求sin∠CBA的值. 第7题 类型三　利用切线与相关半径的关系构造直角三角形 8. (2023·武汉)如图,在四边形ABCD中,AB∥CD,AD⊥AB,以点D为圆心、AD长为半径的弧恰好与BC相切,切点为E.若=,则sinC的值为　　　　. 　　　　　　 9. 如图,半径为的☉O与边长为8的等边三角形ABC的两边AB、BC都相切,连接OC,则tan∠OCB的值为　　　　. 小专题(六)　添设辅助线构造 直角三角形解题 1. A　2. D ... ...