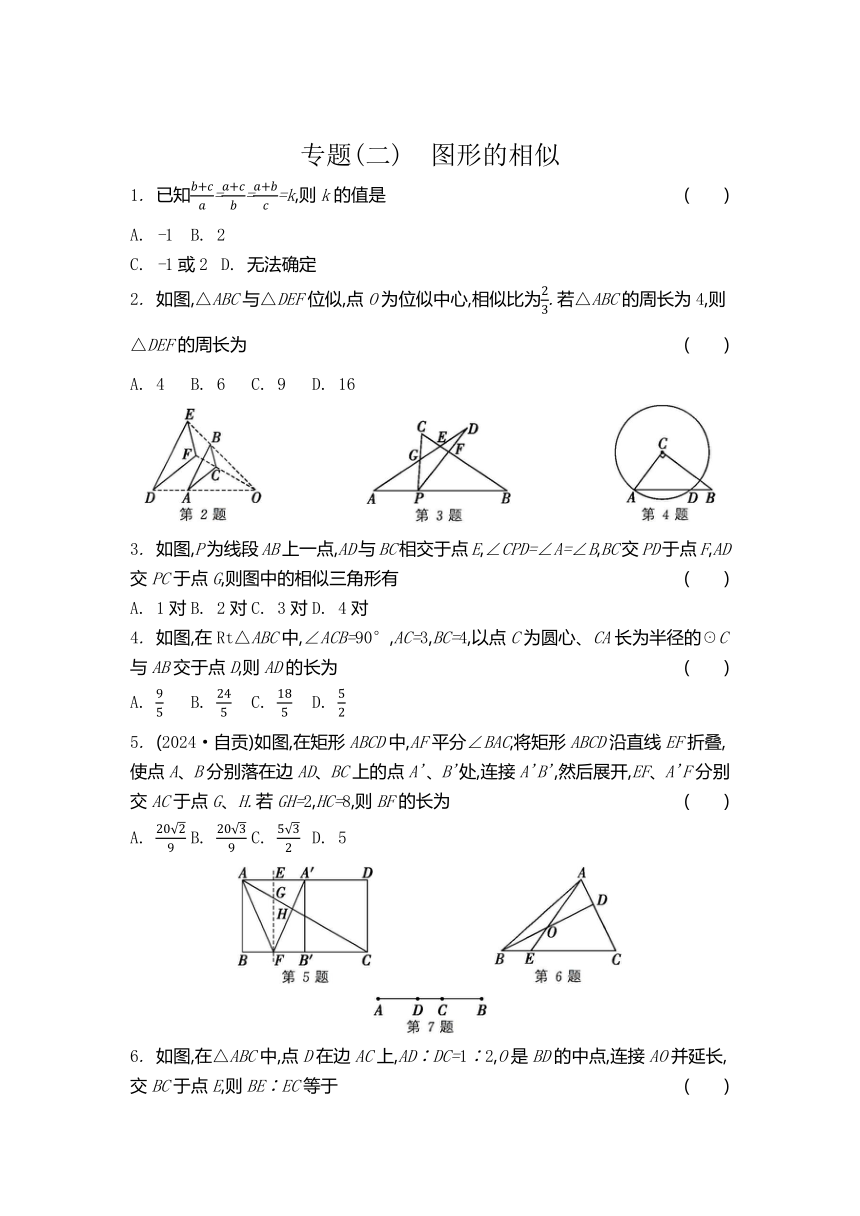
专题(二) 图形的相似 1. 已知===k,则k的值是 ( ) A. -1 B. 2 C. -1或2 D. 无法确定 2. 如图,△ABC与△DEF位似,点O为位似中心,相似比为.若△ABC的周长为4,则△DEF的周长为 ( ) A. 4 B. 6 C. 9 D. 16 3. 如图,P为线段AB上一点,AD与BC相交于点E,∠CPD=∠A=∠B,BC交PD于点F,AD交PC于点G,则图中的相似三角形有 ( ) A. 1对 B. 2对 C. 3对 D. 4对 4. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心、CA长为半径的☉C与AB交于点D,则AD的长为 ( ) A. B. C. D. 5. (2024·自贡)如图,在矩形ABCD中,AF平分∠BAC,将矩形ABCD沿直线EF折叠,使点A、B分别落在边AD、BC上的点A'、B'处,连接A'B',然后展开,EF、A'F分别交AC于点G、H.若GH=2,HC=8,则BF的长为 ( ) A. B. C. D. 5 6. 如图,在△ABC中,点D在边AC上,AD∶DC=1∶2,O是BD的中点,连接AO并延长,交BC于点E,则BE∶EC等于 ( ) A. 1∶2 B. 1∶3 C. 1∶4 D. 2∶3 7. (2023·达州)如图,乐器上的一根弦AB=80cm,两个端点A、B固定在乐器面板上,支撑点C是靠近点B的黄金分割点,支撑点D是靠近点A的黄金分割点,则支撑点C、D之间的距离为 cm(结果保留根号). 8. (2024·云南)如图,AB与CD交于点O,且AC∥BD.若=,则的值为 . 9. 在平面直角坐标系中,点A的坐标是(-2,1),以原点O为位似中心,把线段OA放大为原来的2倍,点A的对应点为A'.若点A'恰在某一反比例函数的图像上,则该反比例函数的表达式为 . 10. 如图,在正方形ABCD中,AB=12,AE=AB,点P在BC上运动(不与点B、C重合),过点P作PQ⊥EP,交CD于点Q,则CQ长的最大值为 . 11. 如图,△ABO的顶点A在函数y=(x>0)的图像上,∠ABO=90°,过AO的三等分点M、N分别作x轴的平行线,交AB于点P、Q.若四边形MNQP的面积为3,则k的值为 . 12. (2024·眉山)如图,菱形ABCD的边长为6,∠BAD=120°,过点D作DE⊥BC,交BC的延长线于点E,连接AE分别交BD、CD于点F、G,则FG的长为 . 13. (2024·苏州)如图,在△ABC中,∠ACB=90°,CB=5,CA=10,点D、E分别在边AC、AB上,AE=AD,连接DE,将△ADE沿DE折叠,得到△FDE,连接CE、CF.若△CEF的面积是△BEC面积的2倍,则AD的长为 . 14. 如图,四边形ABCD为菱形,点E在AC的延长线上,∠ACD=∠EBA. (1) 求证:△ABC∽△AEB; (2) 当AB=6,AC=4时,求AE的长. 第14题 15. (2024·南通改编)如图,在△ABC中,AB=AC=1,BC=,在边AC上截取AD=BC,连接BD. (1) 通过计算,判断AD2与AC·CD的大小关系; (2) 求∠ABD的度数. 第15题 16. (2024·包头)在 ABCD中,∠ABC为锐角,点E在边AD上,连接BE、CE,且S△ABE=S△DCE. (1) 如图①,若F是边BC的中点,连接EF,对角线AC分别与BE、EF相交于点G、H. ① 求证:H是AC的中点; ② 求AG∶GH∶HC. (2) 如图②,BE的延长线与CD的延长线相交于点M,连接AM,CE的延长线与AM相交于点N.试探究线段AM与线段AN之间的数量关系,并证明你的结论. 17. (2024·威海)如图,AB是☉O的直径,点C、D在☉O上,且BC=CD.E是线段AB的延长线上一点,连接EC并延长,交射线AD于点F.∠FEG的平分线EH交射线AC于点H,∠H=45°. (1) 求证:EF是☉O的切线; (2) 若BE=2,CE=4,求AF的长. 第17题 18. 如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴、y轴的正半轴上,点B的坐标是(5,2),P是边CB上一动点(不与点C、B重合),连接OP、AP,过点O作射线OE,交AP的延长线于点E,交边CB于点M,且∠AOP=∠COM,令CP=x,MP=y. (1) 当x为何值时,OP⊥AP (2) 求y与x之间的函数表达式,并写出x的取值范围. (3) 在点P运动的过程中,是否存在x,使△OCM与△ABP的面积之和等于△EMP的面积 若存在,请求出x的值;若不存在,请说明理由. 第18题 专题(二) 图形的相似 1. C ... ...
~~ 您好,已阅读到文档的结尾了 ~~

