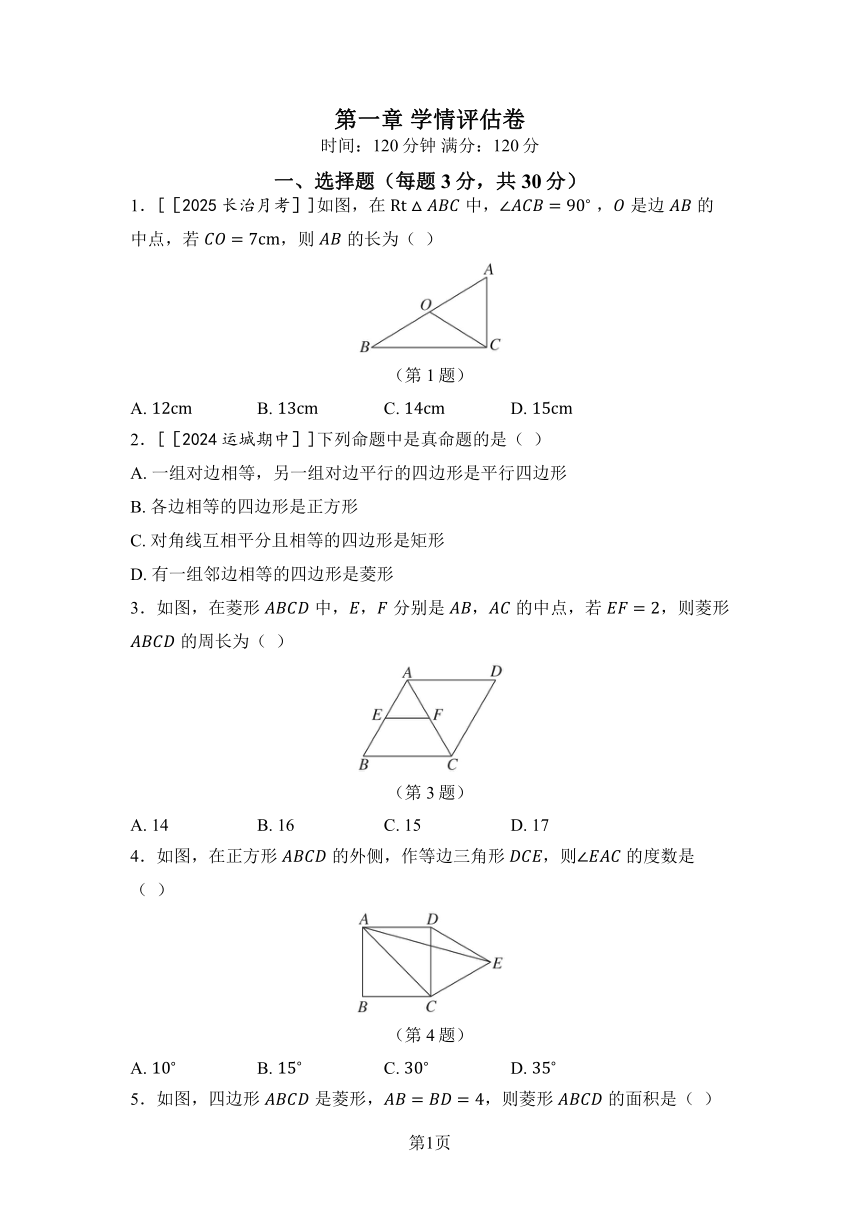
第一章 学情评估卷 时间:120分钟 满分:120分 一、选择题(每题3分,共30分) 1.[[2025长治月考]]如图,在中, ,是边的中点,若,则的长为( ) (第1题) A. B. C. D. 2.[[2024运城期中]]下列命题中是真命题的是( ) A. 一组对边相等,另一组对边平行的四边形是平行四边形 B. 各边相等的四边形是正方形 C. 对角线互相平分且相等的四边形是矩形 D. 有一组邻边相等的四边形是菱形 3.如图,在菱形中,,分别是,的中点,若,则菱形的周长为( ) (第3题) A. 14 B. 16 C. 15 D. 17 4.如图,在正方形的外侧,作等边三角形,则的度数是( ) (第4题) A. B. C. D. 5.如图,四边形是菱形,,则菱形的面积是( ) (第5题) A. B. 16 C. D. 6.如图,在矩形 中,对角线 与 相交于点,,,则 的度数为( ) (第6题) A. B. 或 C. D. 或 7.如图①,小强拿一张正方形的纸,沿虚线对折一次得图②,再沿虚线对折一次得图③,然后用剪刀沿图③中的虚线剪去一个角,最后打开后的形状是( ) (第7题) A. B. C. D. 8.[[2025晋中月考]]如图,,,,分别为四边形的边,,,的中点,连接,,要使四边形为矩形,应添加的条件是( ) (第8题) A. B. C. D. 9.如图,在正方形 中,为 边上一点,且.将 绕点 逆时针旋转 得到,连接,,则线段 的长度是( ) (第9题) A. B. C. 2 D. 10.如图,在矩形 中,,,,为对角线 上的点,且满足,连接,,则 的最小值为( ) (第10题) A. 6 B. C. D. 10 二、填空题(每题3分,共15分) 11.菱形一般有_ _ _ _ _ _ 条对称轴. 12.如图,矩形在平面直角坐标系内,点的坐标为,则对角线的长为_ _ _ _ _ _ . (第12题) 13.如图,是 的角平分线,交 于,交 于,且 交 于,则 的度数是_ _ _ _ _ _ _ _ . (第13题) 14.如图,在四边形 中, ,,于.若四边形 的面积是18,则 的长是_ _ _ _ _ _ _ _ . (第14题) 15.如图,在矩形纸片 中,,,点 在边 上.将纸片沿 折叠,点 落在点 处.当点 在对角线 上时,的长为_ _ _ _ . (第15题) 三、解答题(共75分) 16.[[2025太原月考]](8分) 如图,在矩形中,对角线与相交于点,,,垂足分别为,.求证:. 17.(8分)如图,在菱形中,,分别是,边上的点,连接,,,.求证:. 18.(8分)如图,在正方形中,点为边上一点,点为延长线上一点,且,则与之间有怎样的数量关系和位置关系?请说明理由. 19.(8分)如图,已知在中,,是边上的中线,,分别是,的中点,为延长线上的点,连接,,. (1) 求证:; (2) 求证:四边形是矩形. 20.(8分)如图,在中,,相交于点,点,在上,. (1) 求证:四边形是平行四边形; (2) 若,,求证:四边形是正方形. 21.(10分) 下面是小清同学的数学笔记,仔细阅读并回答问题. 在平行四边形 中,,求作菱形,使点、点 分别在、边上. 方法一:以点 为圆心,长为半径画弧,交 于点,再分别以点、为圆心,大于 的长为半径画弧,两弧交于点,连接 并延长交 于点,连接,则四边形 是菱形,如图①. 方法二:连接,分别以点、为圆心,大于 的长为半径画弧,两弧交于、两点,作直线,分别与、、交于、、三点,连接、,则四边形 是菱形. (1) 填空:“方法一”中,判定四边形是菱形的数学依据是_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ ; (2) 在图②中,根据“方法二”的作图方法,使用直尺和圆规补全图形(保留作图痕迹); (3) 写出“方法二”的推理过程. 22.(12分)综合与实践 【问题背景】 在一次综合与实践课上,老师让同学们以两张全等的三角形纸片为操作对象,进行相关问题的研究,下面是创新小组在操 ... ...
~~ 您好,已阅读到文档的结尾了 ~~