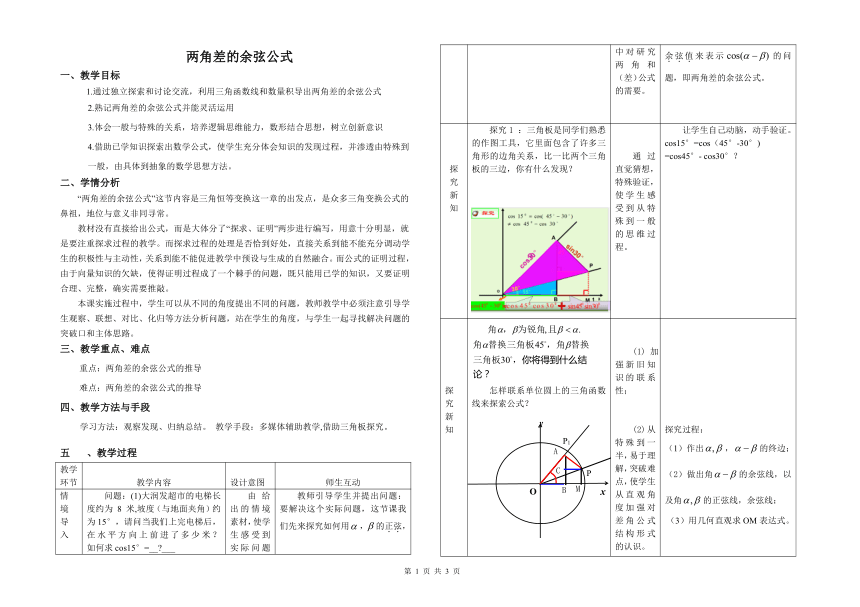
两角差的余弦公式 一、教学目标 1.通过独立探索和讨论交流,利用三角函数线和数量积导出两角差的余弦公式 2.熟记两角差的余弦公式并能灵活运用 3.体会一般与特殊的关系,培养逻辑思维能力,数形结合思想,树立创新意识 4.借助已学知识探索出数学公式,使学生充分体会知识的发现过程,并渗透由特殊到 一般,由具体到抽象的数学思想方法。 二、学情分析 “两角差的余弦公式”这节内容是三角恒等变换这一章的出发点,是众多三角变换公式的鼻祖,地位与意义非同寻常。 教材没有直接给出公式,而是大体分了“探求、证明”两步进行编写,用意十分明显,就是要注重探求过程的教学。而探求过程的处理是否恰到好处,直接关系到能不能充分调动学生的积极性与主动性,关系到能不能促进教学中预设与生成的自然融合。而公式的证明过程,由于向量知识的欠缺,使得证明过程成了一个棘手的问题,既只能用已学的知识,又要证明合理、完整,确实需要推敲。 本课实施过程中,学生可以从不同的角度提出不同的问题,教师教学中必须注意引导学生观察、联想、对比、化归等方法分析问题,站在学生的角度,与学生一起寻找解决问题的突破口和主体思路。 三、教学重点、难点 重点:两角差的余弦公式的推导 难点:两角差的余弦公式的推导 四、教学方法与手段 学习方法:观察发现、归纳总结。 教学手段:多媒体辅助教学,借助三角板探究。 五、教学过程 教学环节 教学内容 设计意图 师生互动 情境导入 问题:(1)大润发超市的电梯长度约为 8 米,坡度(与地面夹角)约为15°,请问当我们上完电梯后,在水平方向上前进了多少米? 如何求cos15°=__ ___ 由给出的情境素材,使学生感受到实际问题中对研究两角和(差)公式的需要。 教师引导学生并提出问题:要解决这个实际问题,这节课我们先来探究如何用,的正弦,余弦值来表示的问题,即两角差的余弦公式。 探究新知 探究1 :三角板是同学们熟悉的作图工具,它里面包含了许多三角形的边角关系,比一比两个三角板的三边,你有什么发现? 通过直觉猜想,特殊验证,使学生感受到从特殊到一般的思维过程。 让学生自己动脑,动手验证。cos15°=cos(45°-30°)=cos45°- cos30°? 探究新知 怎样联系单位圆上的三角函数线来探索公式? 加强新旧知识的联系性;(2)从特殊到一半,易于理解,突破难点,使学生从直观角度加强对差角公式结构形式的认识。 探究过程:(1)作出,的终边;(2)做出角的余弦线,以及角的正弦线,余弦线;(3)用几何直观求OM表达式。注意:以上结果是在,都是锐角,且的情况下得到的,所得结果是否对任意角都成立,结论是肯定的,可以让同学们课下完成。 探究2:上面通过回归定义,我们推导出了两角差的余项公式,还有其他方法吗?前面所学的什么知识中有角的余弦 能否利用向量方法探究?(1)在直角坐标系中作单位圆O,以为始边作角,它们的终边分别交单位圆于点,并标出角。(2),,(3),由向量的夹角公式得出 让学生经历用向量知识解出一个数学问题的过程,体会向量方法的作用。同学们通过比较发现向量法更简单,认识到向量是重要的数学工具。 (1)先结合图形,让学生明确应选择哪几个向量,自己动手表示;(2)学生回顾向量的夹角公式,并求得探究结果;(3)教师引导学生对探索过程进一步严格化的思考和处理。由向量数量积的概念,角;由于都是任意角,也是任意角,但是由诱导公式,总有一个角,使 若,为的夹角, = 若,则为的夹角,=(以上推导是否有不严谨之处?应如何补充?) 发现结论 (两角差的余弦公式):对于任意角,都有 使学生进一步熟悉公式,了解公式的结构特征。 师生共同分析公式结构特点:烤烤晒晒符号反,简记为 知识应用 例1:用差角余弦公式求的值。解法1:解法 ... ...
~~ 您好,已阅读到文档的结尾了 ~~