根据旋转的性质求解综合题典型题型 归纳练 2025年中考数学二轮复习备考

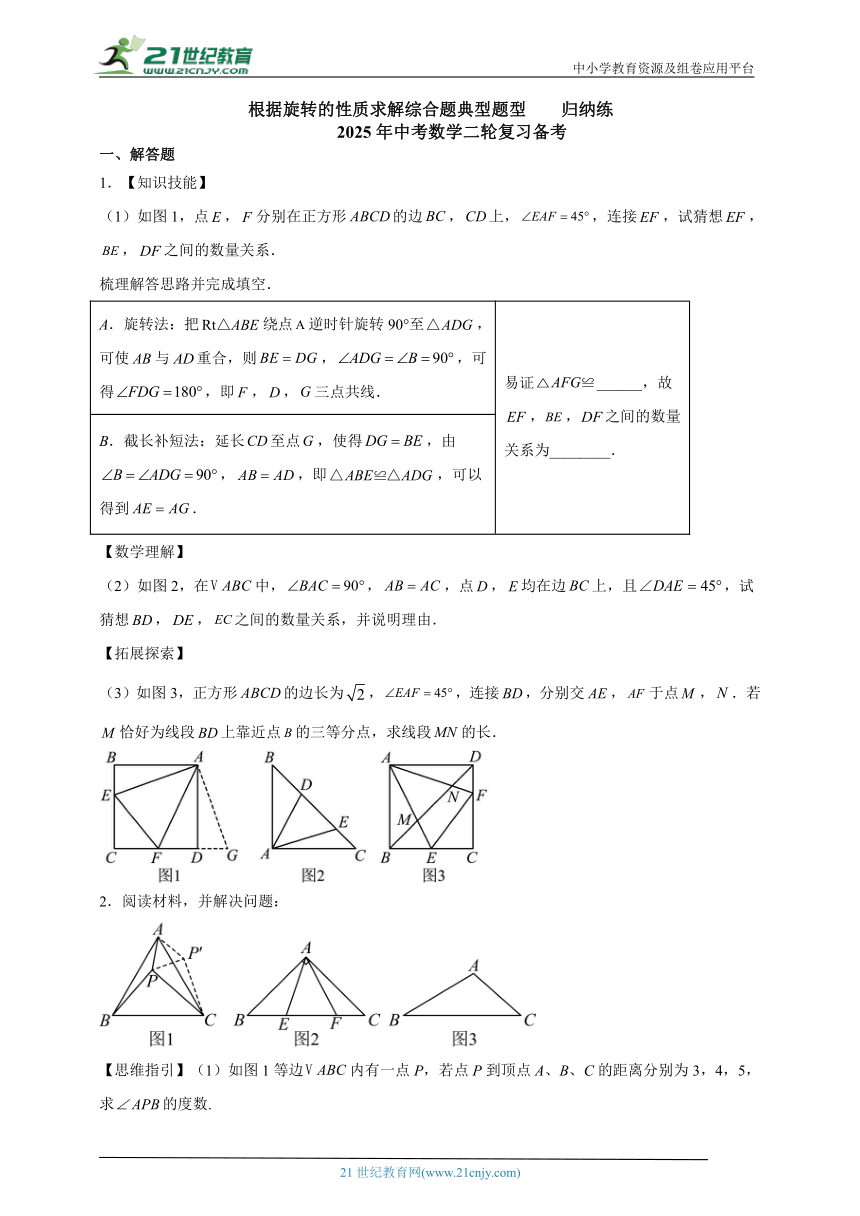
中小学教育资源及组卷应用平台 根据旋转的性质求解综合题典型题型 归纳练 2025年中考数学二轮复习备考 一、解答题 1．【知识技能】 （1）如图1，点，分别在正方形的边，上，，连接，试猜想，，之间的数量关系． 梳理解答思路并完成填空． A．旋转法：把绕点逆时针旋转90°至，可使与重合，则，，可得，即，，三点共线． 易证_____，故，，之间的数量关系为_____． B．截长补短法：延长至点，使得，由，，即，可以得到． 【数学理解】 （2）如图2，在中，，，点，均在边上，且，试猜想，，之间的数量关系，并说明理由． 【拓展探索】 （3）如图3，正方形的边长为，，连接，分别交，于点，．若恰好为线段上靠近点的三等分点，求线段的长． 2．阅读材料，并解决问题： 【思维指引】（1）如图1等边内有一点P，若点P到顶点A、B、C的距离分别为3，4，5，求的度数. 解决此题，我们可以将绕顶点A旋转到处，此时，连接，借助旋转的性质可以推导出是_____三角形；这样利用旋转变换，我们将三条线段 转化到一个三角形中，从而求出_____； 【知识迁移】（2）如图2，在中，，，E、F为上的点且，请判断，，的数量关系，并证明你的结论. 【方法推广】（3）如图3，在中，，，，点P为内一点，连接，直接写出的最小值. 3．以“图形的旋转”为主题的数学活动课上，同学们尝试使用三角形纸板开展探究活动．如图，在中，，，，取，中点，，将沿剪开，得到四边形和，将绕点顺时针旋转得到． 【操作发现】（1）若交于点，求证：； 【深入探索】（2）在（）的条件下，同学们发现将旋转到一些特殊位置时，可以进一步探索线段长度． 如图，若，求的长； 如图，若，，三点共线，求的长； 【拓展延伸】（3）在旋转的过程中，请直接写出面积的最大值． 4．如图1，在中，，，DE是的中位线．将绕点A按顺时针方向旋转，射线BD与射线CE交于点P，如图2所示． (1)求证：． (2)在这个旋转过程中，的度数是否发生改变？若不变，求出的度数；若改变，请说明理由． (3)当时，求BP的长． 5．【问题情境】 某数学活动小组在研究菱形对角线上的动点问题时提出如下思路： 在菱形中，对角线，交于点M，且，G是线段上的动点（不与点M，B重合），，E是线段的中点，绕点E顺时针旋转，得到线段．连接，，． （1）如图1，当点E在直线上，且时． ①求证：； ②求证：． 【拓展迁移】 （2）如图2，当点E不在直线上，且时，的结论是否仍成立，若成立，请写出证明过程，若不成立，请说明理由． 6．如图①是实验室中的一种摆动装置，在地面上，支架是底边为的等腰直角三角形，摆动臂可绕点旋转，摆动臂可绕点旋转，，． (1)在旋转过程中， ①当，，三点在同一直线上时，的长为 ； ②当，，三点为同一直角三角形的顶点时，求的长； (2)若摆动臂顺时针旋转，点的位置由外的点，转到其内的点处，即满足，连接，如图②，此时，求的长． 7．当几何图形中，两个共顶点的角所在角度是公共大角一半的关系，我们称之为“半角模型”，通常用“旋转的观点”看待图形的几何变换，使得两个分散的角变换成为一个三角形，相当于构造出两个三角形全等． 【问题初探】 （1）如图1，在四边形中，，、分别是、边上的点，且，求出图中线段之间的数量关系． 如图1，从条件出发：将绕着点逆时针旋转到位置，根据“旋转的性质”分析与之间的关系，再通过全等的性质得到线段之间的数量关系，可证得结论． 【类比分析】 （2）如图2，在四边形中，，，，且，，，求的长． 【学以致用】 （3）如图3，在四边形中，，与互补，点、分别在射线、上，且．当时，求出的周长． 8．综合与实践 【思考尝试】 （1）如图①，在中，，点在上，连接，将线段绕点逆时针旋转得到线段，连接，．用等式写出线段，，的数量关系，并说 ... ...