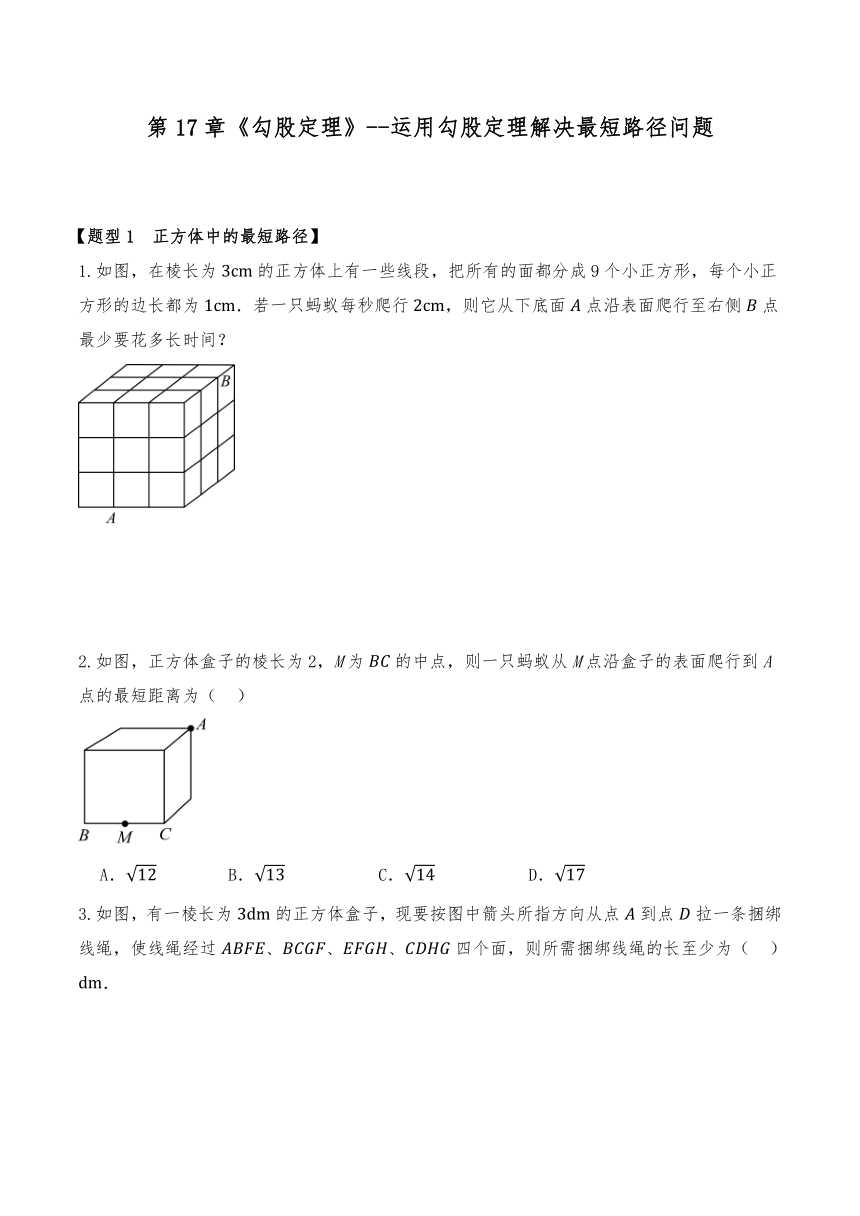
第17章《勾股定理》--运用勾股定理解决最短路径问题 【题型1 正方体中的最短路径】 1.如图,在棱长为的正方体上有一些线段,把所有的面都分成9个小正方形,每个小正方形的边长都为.若一只蚂蚁每秒爬行,则它从下底面点沿表面爬行至右侧点最少要花多长时间? 2.如图,正方体盒子的棱长为2,M为的中点,则一只蚂蚁从M点沿盒子的表面爬行到A点的最短距离为( ) A. B. C. D. 3.如图,有一棱长为的正方体盒子,现要按图中箭头所指方向从点到点拉一条捆绑线绳,使线绳经过、、、四个面,则所需捆绑线绳的长至少为( ). A. B. C. D. 4.棱长分别为两个正方体如图放置,点P在上,且,一只蚂蚁如果要沿着长方体的表面从点A爬到点P,需要爬行的最短距离是 . 【题型2 长方体中的最短路径】 1.如图是一块长、宽、高分别是和的长方体木块,一只蚂蚁要从长方体木块的一个顶点处,沿着长方体的表面到长方体上和顶点相对的顶点处吃食物,那么它需要爬行的最短路径的长是( ) A. B. C. D. 2.如图,一个长方体建筑物的长、宽、高分别为3米、1米和6米,为了美观,现要在该建筑物上缠绕灯线以便安装小彩灯,灯线的绕法是从下底面的顶点开始经过四个侧面绕到上底面的顶点,如果缠绕的圈数是,那么用在该建筑物上的灯线最短需要 米. 3.如图,在一个边长为的正方形纸片上,放着一根长方体木块,已知该木块的较长边与平行,横截面是边长为的正方形,一只蚂蚁从点A爬过木块到达蜂蜜C处需爬行的最短路程是 . 4.如图,一个长方体蛋糕盒的长、宽、商分别为,点到点的距离为.现有一只蚂蚁从点出发,沿着长方体的表面爬行到点处,则蚂蚁需要爬行的最短距离是( ) A. B. C. D. 【题型3 圆柱中的最短路径】 1.如图,动点从点出发,沿着圆柱的侧面移动到的中点,若,点P移动的最短距离为,则圆柱的底面周长为( ) A. B. C. D. 2.如图,已知圆柱底面的周长为,圆柱高为,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为 . 3.如图,圆柱底面圆的周长为6cm,CD、AB分别是上、下底面的直径,高,用一条无弹性的丝带从A至C按如图所示的圈数缠绕,则丝带的最短长度为 cm. 4.如图所示,已知圆柱的底面周长为36,高,点位于圆周顶面处,小虫在圆柱侧面爬行,从点爬到点,然后再爬回点,则小虫爬行的最短路程为 . 【题型4 圆锥中的最短路径】 1.已知圆锥的底面半径是,母线长为,C为母线的中点,蚂蚁在圆锥侧面上从A爬到C的最短距离是 . 2.如图,小明用半径为20,圆心角为的扇形,围成了一个底面半径r为5的圆锥. (1)扇形的圆心角为 ; (2)一只蜘蛛从圆锥底面圆周上一点A出发,沿圆锥的侧面爬行一周后回到点A的最短路程是 . 3.某班学生表演课本剧,要制作一顶圆锥形的小丑帽.如图,这个圆锥的底面圆周长为 ,母线长为30,为了使帽子更美观,要粘贴彩带进行装饰,其中需要粘贴一条从点A处开始,绕侧面一周又回到点A的彩带(彩带宽度忽略不计),这条彩带的最短长度是( ) A. B. C. D. 4.如图,圆锥的轴截面是边长为6cm的正三角形ABC,P是母线AC的中点,则在圆锥的侧面上从B点到P点的最短路线的长为( ) A. B.2 C.3 D.4 【题型5 台阶中的最短路径】 1.如图是一个二级台阶,每一级台阶的长、宽、高分别为、、.和是台阶两个相对的端点,在点有一只蚂蚁,想到点去觅食,那么它爬行的最短路程是( ) A. B. C. D. 2.如图,学校实验楼前一个三级台阶,它的每—级的长、宽、高分别为24dm,3dm,3dm,点M和点N是这个台阶上两个相对的端点,M点有一只蚂蚁,想到N点处去吃可口的食物,则蚂蚁沿着台阶面爬行到点N的最短路程( ) A. B. C. D. 3.如图,是一个三级台阶,它每一级长,宽,高分别为4, ... ...
~~ 您好,已阅读到文档的结尾了 ~~