旋转压轴精选题特训（含解析）-2025年中考数学二轮专题

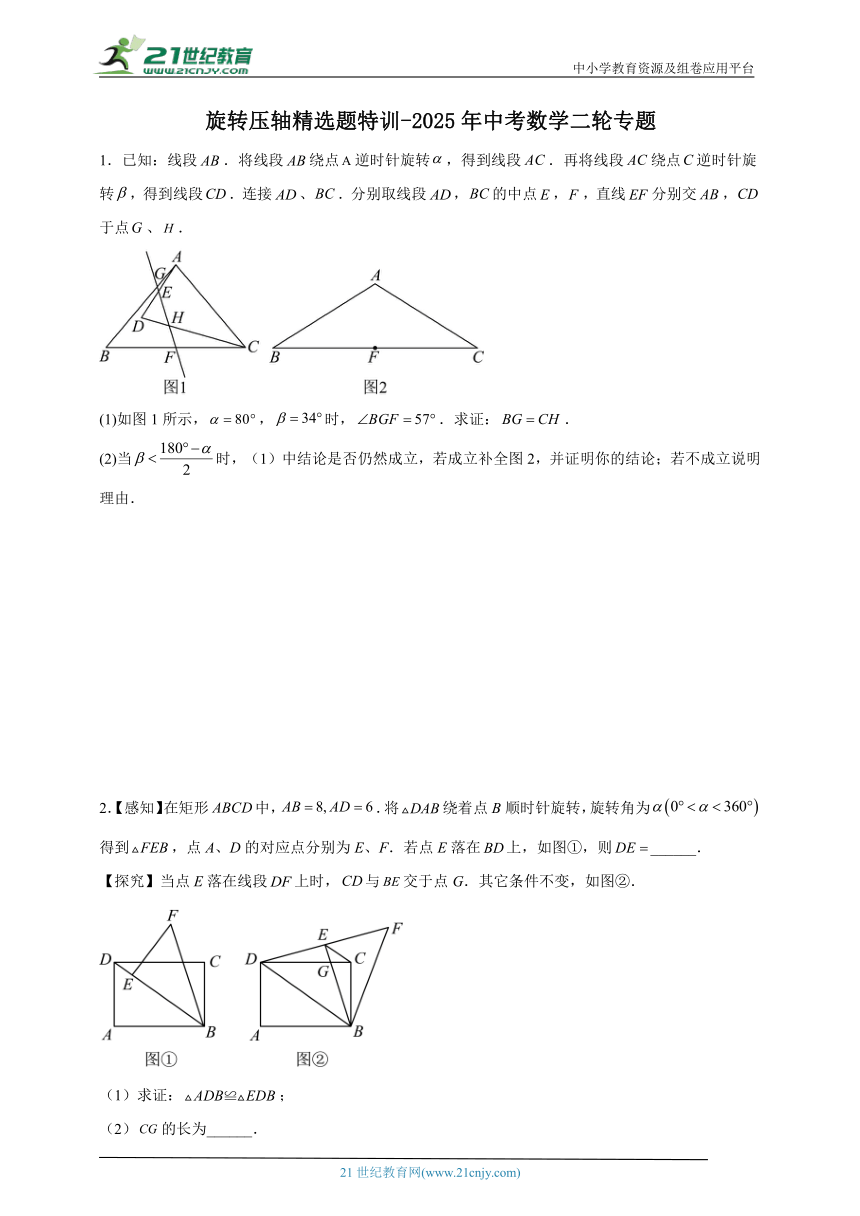
中小学教育资源及组卷应用平台 旋转压轴精选题特训-2025年中考数学二轮专题 1．已知：线段．将线段绕点逆时针旋转，得到线段．再将线段绕点逆时针旋转，得到线段．连接、．分别取线段，的中点，，直线分别交，于点、． (1)如图1所示，，时，．求证：． (2)当时，（1）中结论是否仍然成立，若成立补全图2，并证明你的结论；若不成立说明理由． 2．【感知】在矩形中，．将绕着点B顺时针旋转，旋转角为得到，点A、D的对应点分别为E、F．若点E落在上，如图①，则_____． 【探究】当点E落在线段上时，与交于点G．其它条件不变，如图②． （1）求证：； （2）的长为_____． 【拓展】连接，在的旋转过程中，设的面积为S，直接写出S的取值范围． 3．在矩形中，，，以点A为旋转中心，逆时针旋转矩形，旋转角为（），得到矩形，点B、点C、点D的对应点分别为点E、点F、点G． (1)如图①，当点E落在边上时，求线段EC的长度； (2)如图②，当点E落在线段上时，与相交于点H，连接． ①求证：； ②求线段的长度． (3)如图③设点P为边的中点，连接，，在矩形旋转过程中，的面积是否存在最大值？若存在，请直接写出这个最大值；若不存在，请说明理由． 4．小轩家有一个如图1所示的正方体家用医药箱，其侧面是如图2所示的正方形，在打开医药箱的过程中，矩形（箱盖）可以绕点逆时针旋转，落在的位置，且，． (1)如图2，当旋转角为时，求点与点之间的距离． (2)若矩形在旋转过程中，可旋转的最大角度是，求点到的最大距离．（参考数据：，，） 5．如图1，在中，，，，于点，为上一动点，连接，将线段绕点逆时针旋转得到线段，连接． (1)如图2，当点为线段的中点时，点与点重合，则线段和之间的数量关系是_____． (2)如图1，当时，写出线段，和之间的数量关系，并说明理由． 6．问题背景：如图1，设P是等边内一点，，，，求的度数．小君研究这个问题的思路是：将绕点A逆时针旋转得到，易证：是等边三角形，是直角三角形，所以． 简单应用： (1)如图2，在等腰直角中，，P为内一点，且，，，则_____°． (2)如图3，在等边中，P为内一点，且，，，求长． (3)拓展延伸：若图4中的等腰直角，与，，在的同侧，若，，求的长度． 7．已知与均为等边三角形，且顶点A重合，现将等边绕顶点A转动得到下列图形． (1)初步探究：如图1，连接、，当、、三点在同一直线上时，猜想， 请证明这一结论是正确的； (2)大胆尝试：如图2，连接、，当、、三点在同一直线上时，作于H，猜想、与的数量关系并证明你猜想的结论． (3)拓展延伸：如图3，连接、，当时，延长交于点F，过点D作于，，的面积为，求的长． 8．【问题情境】 数学活动课上，老师和同学们一起玩旋转，如图1，四边形是正方形，绕点顺时针旋转后与重合． 【解决问题】 （1）连接，若，，求的长； 【类比迁移】 （2）用上述思想或其他方法证明：如图2，在正方形中，点、分别在、上，且．求证：． 9．如图，在正方形中，点E，F分别在边和上，且，连接，分别交，于点H，点G，连接，，． (1)若正方形的边长为，则的周长为_____； (2)求证：； (3)与存在怎样的位置关系？请说明理由； (4)求证：为定值． 10．如图1，是大家非常熟悉的“一线三直角模型”，受到这模型的启发，我们研究如下问题：如图2，在中，，将线段绕点B顺时针旋转得到线段，作交的延长线于点E，连接并延长交的延长线于点F， (1)若，求线段的长； (2)在（1）的条件下，连接交于点N，求的值； (3)在（1）的条件下，在直线上找点P，使，直接写出线段的长度． 11．如图，在平行四边形中，O为的中点，直线l与边重合，将直线l绕点B旋转，旋转角为，直线l于点M，直线l于点N，连接、． (1)如图①，当直线l绕点B逆时针旋转（）时，请直接写出、的数量关系是 ... ...