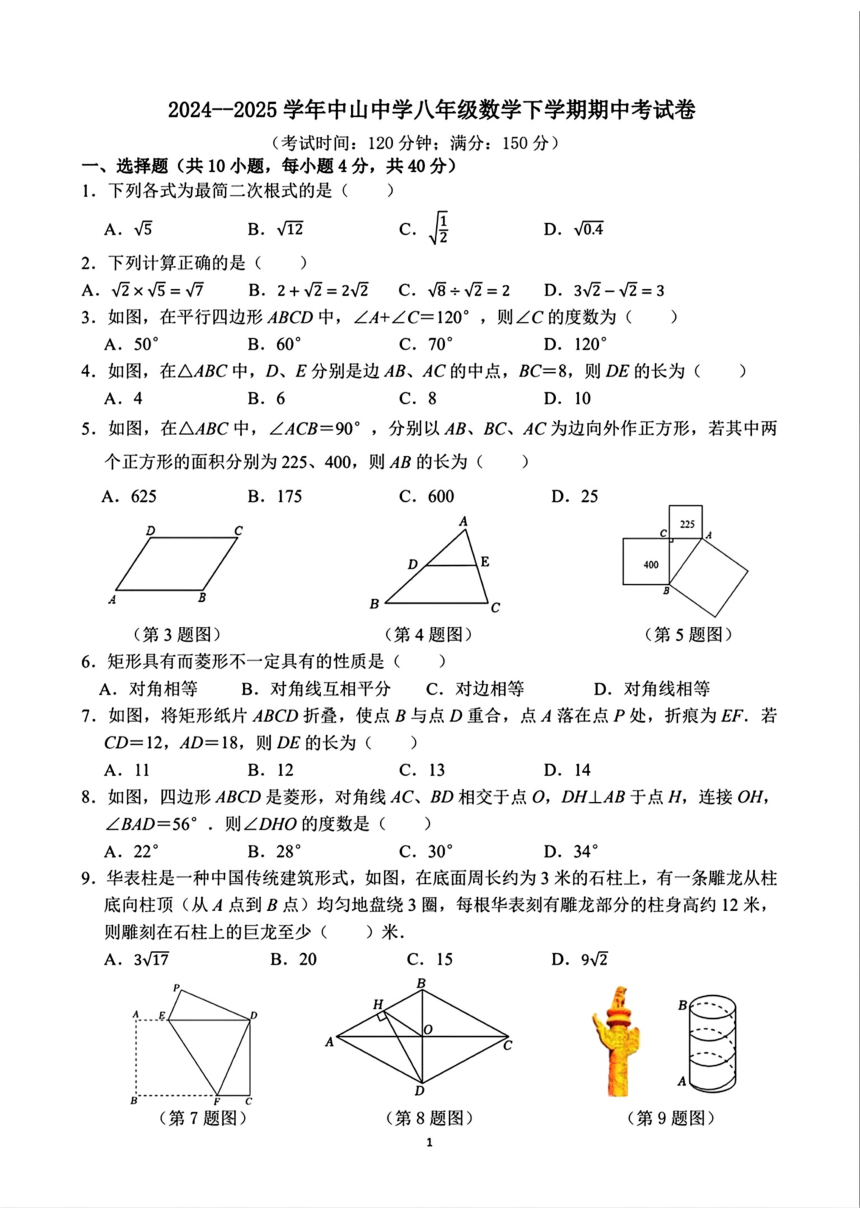
2024-2025学年中山中学八年级数学下学期期中考试卷 (考试时间:120分钟:满分:150分) 一、选择题(共10小题,每小题4分,共40分) 1.下列各式为最简二次根式的是() A.5 B.V12 c. D.0.4 2.下列计算正确的是() A.V2×V5=√7 B.2+V2=22C.V⑧÷2=2 D.3V2-V2=3 3.如图,在平行四边形ABCD中,∠A+∠C=120°,则∠C的度数为() A.50° B.60° C.70° D.120° 4.如图,在△ABC中,D、E分别是边AB、AC的中点,BC=8,则DE的长为() A.4 B.6 C.8 D.10 5.如图,在△ABC中,∠ACB=90°,分别以AB、BC、AC为边向外作正方形,若其中两 个正方形的面积分别为225、400,则AB的长为() A.625 B.175 C.600 D.25 A 225 D E 400 (第3题图) (第4题图) (第5题图) 6.矩形具有而菱形不一定具有的性质是() A.对角相等 B.对角线互相平分 C.对边相等 D.对角线相等 7.如图,将矩形纸片ABCD折叠,使点B与点D重合,点A落在点P处,折痕为EF.若 CD=12,AD=18,则DE的长为() A.11 B.12 C.13 D.14 8.如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于点H,连接OH, ∠BAD=56°,则∠DHO的度数是() A.22° B.28° C.30° D.34° 9.华表柱是一种中国传统建筑形式,如图,在底面周长约为3米的石柱上,有一条雕龙从柱 底向柱顶(从A点到B点)均匀地盘绕3圈,每根华表刻有雕龙部分的柱身高约12米, 则雕刻在石柱上的巨龙至少()米 A.317 B.20 C.15 D.9v2 B H (第7题图) (第8题图) (第9题图) 1 10.勾股定理是人类最伟大的科学发现之一,最早是由中国西周数学家商高发现并证明的, 早于西方五百到六百年,关于勾股定理的证明方法有很多,以下是出自于古代的一种证 法.过正方形对角线交点做两条互相垂直的线段,将正方形分成四块四边形,如图1,然 后将其拼成一个大正方形ABCD,如图2,若阴影部分图形面积为16, EG 5 FG=2则GH的 长为( ) A.2 B. 3 C.3 D.5 H 二、填空题(共6小题,每小题4分,共24分) 图1 图2 11.若二次根式Vx一9在实数范围内有意义,则x的取值范围是 12.若最简二次根式√m+1与V3是同类二次根式,则m= 13.如图,在正方形ABCD中,E为对角线AC上一点,连接BE,DE,若∠ABE=25°,则 ∠CED的度数为 14.如图,在矩形OCDE中,点D的坐标是(1,3),则CE的长是 15.如图,E,F分别是口ABCD边AD,BC上的点,AF与BE相交于点P,DF与CE相交 于点2,若S△ABP=13cm2,S△cpQ=14cm2,则阴影部分四边形EPF2的面积为 cm2. 16.如图,四边形ABCD为菱形,AB=4,∠ABC=60°,E,F为BD上的两个动点,且 EF=BD,点M是AD的中点,连接CE,MF,则CE+MF的最小值为 (第13题图) (第14题图) (第15题图) (第16题图) 三、解答题(共9小题,共86分) 17.(8分)计算:24÷V3-(⑤+V32. 18.(8分)已知:如图,在口ABCD中,E、F是对角线BD上不同的两点,且BE=DF. 求证:四边形AECF是平行四边形. 2
~~ 您好,已阅读到文档的结尾了 ~~