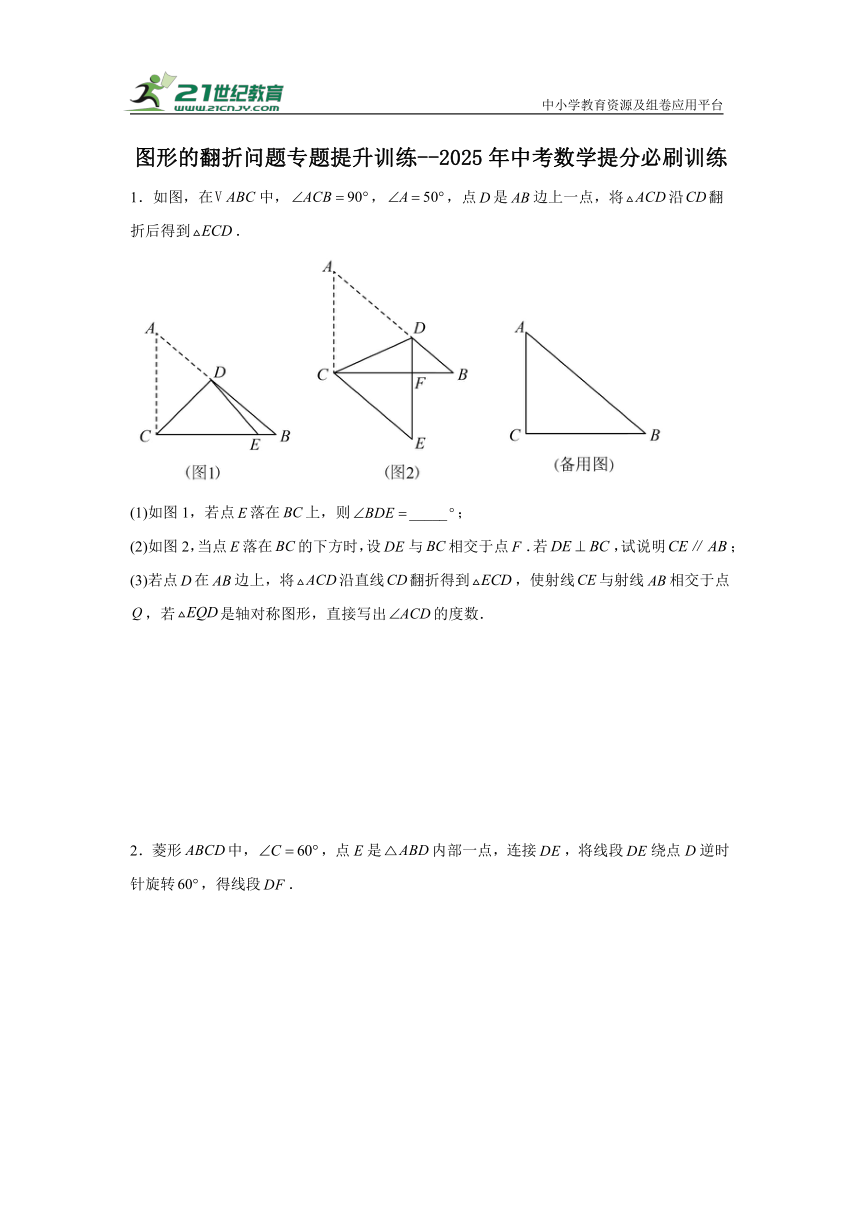
中小学教育资源及组卷应用平台 中小学教育资源及组卷应用平台 图形的翻折问题专题提升训练--2025年中考数学提分必刷训练 1.如图,在中,,,点是边上一点,将沿翻折后得到. (1)如图1,若点落在上,则_____; (2)如图2,当点落在的下方时,设与相交于点.若,试说明; (3)若点在边上,将沿直线翻折得到,使射线与射线相交于点,若是轴对称图形,直接写出的度数. 2.菱形中,,点E是内部一点,连接,将线段绕点D逆时针旋转,得线段. (1)如图1,若三点共线,平分,.求的长; (2)如图2,三点共线,取的中点M,连接并延长交的延长线于点N,若,猜想线段应满足的数量关系,并说明理由; (3)如图3,点H为直线上一动点,连接,将沿直线翻折得到,连接,,若,,当的长度为最小时,请直接写出的最小值. 3.如图1,在一张正方形纸片(正方形的两组对边分别平行)的两边上分别有两点,连接,点是正方形纸片上一点,过点翻折纸片,使点落在直线上的点处,折痕交于点. (1)①_____; ②通过不断地尝试,除了上面的折法,过点再也折不出其它折痕与有①中的位置关系,其中的数学道理是_____: (2)在图1的基础上,展平纸片,得到图2,在图2中过点折出并画出与平行的折痕(折痕左端点记为点,右端点记为点),请简要阐述折叠方法并说明理由; (3)将图2的纸片展平得到图3,点是线段上一动点(不与点重合),若,,请直接写出的度数.(用、的代数式表示) 4.如图,平行四边形中,点为的中点,连接. (1)如图1,连接交于点,求的值; (2)如图2,点在上,连接.若,,,,求的长; (3)如图3,将沿翻折,得到,连接、,若,,,则的值为_____. 5.如图1,四边形的对角线,相交于点O,. (1)在图1中,过点A作交于点E,求证:; (2)如图2,将沿AB翻折得到. ①求证:; ②若,,求的长. 6.如图,在平面直角坐标系中,四边形的顶点分别为点,,,,点从点出发沿轴正方向以每秒1个单位移动,运动了秒,连接并延长交轴于点;将沿直线翻折到,延长与轴交于点. (1)求证:; (2)当时,求的长; (3)当时,求点的坐标(用含的式子表示) 7.已知为等边三角形,是边上一点,连接,点为上一点,连. (1)如图1,延长交于点,若,,求的长; (2)如图2,将绕点顺时针旋转到,延长至点,使得,连接交于点,求证; (3)如图3,,点是上一点,且,连接,点是上一点,,连接,,将沿翻折到,连接,当的周长最小时,直接写出的面积. 8.已知长方形纸片,E为线段上一点,射线交线段于点F,将三角形沿翻折,点A落在点M处;射线交边于点G,将三角形沿翻折,点B落在N处. (1)点E,M,N共线时,如图1,求的度数; (2)点E,M,N不共线时,如图2,若设,,请写出图2中,满足的数量关系式.并说明理由; (3)如图3,设运动时间为t秒,若射线从绕点E以每秒顺时针旋转,当时,点F与D重合,射线停止旋转,若射线从绕点E以每秒逆时针旋转,当时,点G与C重合,射线停止旋转;两条射线同时开始旋转,当t为多少时,? 9.已知是等边三角形,点是外一点,连接,,. (1)如图1,点在的左上方,点是上一点,连接,满足,延长交于点,若,求的度数; (2)如图2,在(1)的条件下,过点作的垂线交于点,求证:; (3)如图3,点在的左侧时,,,点为直线上一动点(点与点不重合),连接,将沿所在直线翻折至所在平面内得到,点为点的对应点,当以点、点、点为顶点构成等腰三角形时,请直接写出此时的值. 10.如图1,四边形是平行四边形,延长至点,使得,连接和. (1)求证:四边形是平行四边形; (2)如图2,将沿直线翻拆点刚好落在线段的中点处,延长与的延长线相交于点,并且和交于点,试求线段、、之间的数量关系; (3)如图3,将沿直线翻折,点刚好落在线段上的点处,若,,且,求 ... ...
~~ 您好,已阅读到文档的结尾了 ~~