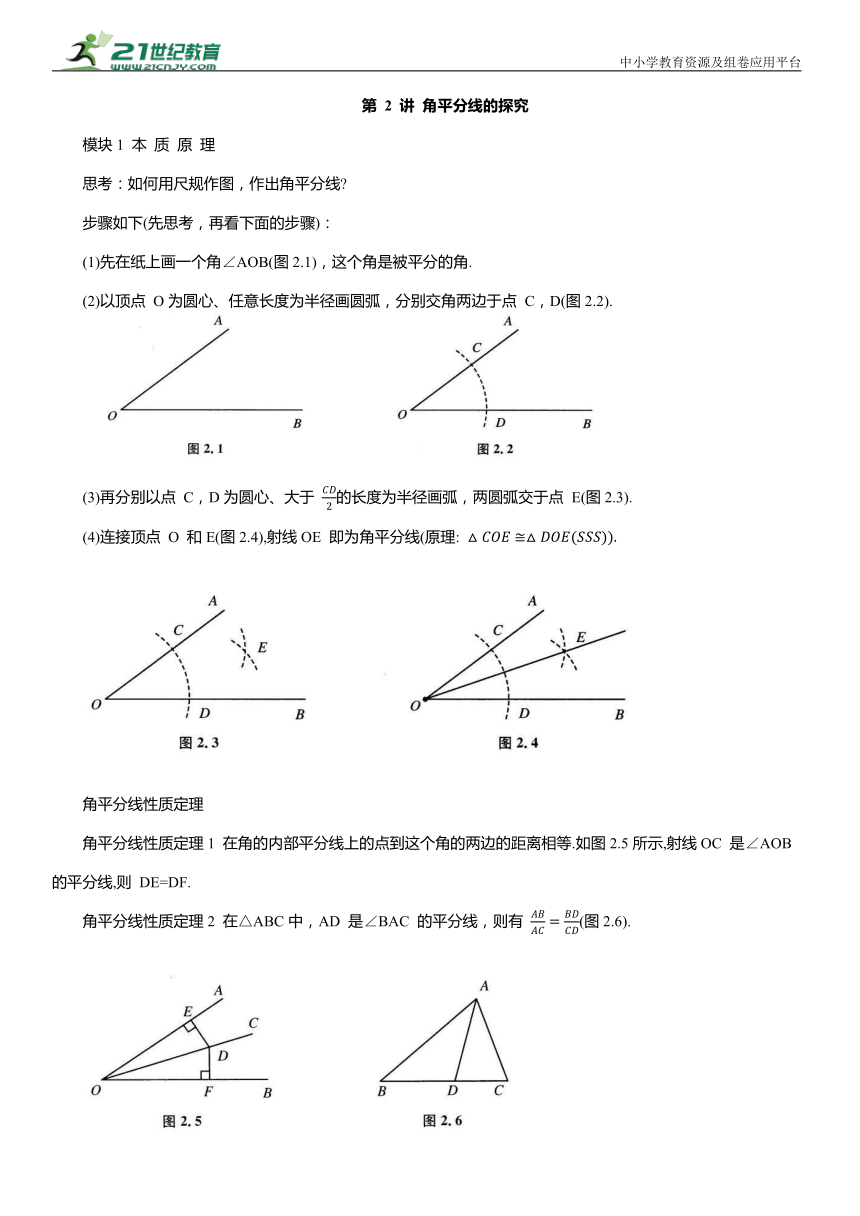
第 2 讲 角平分线的探究 模块1 本 质 原 理 思考:如何用尺规作图,作出角平分线 步骤如下(先思考,再看下面的步骤): (1)先在纸上画一个角∠AOB(图2.1),这个角是被平分的角. (2)以顶点 O为圆心、任意长度为半径画圆弧,分别交角两边于点 C,D(图2.2). (3)再分别以点 C,D为圆心、大于 的长度为半径画弧,两圆弧交于点 E(图2.3). (4)连接顶点 O 和E(图2.4),射线OE 即为角平分线(原理: 角平分线性质定理 角平分线性质定理1 在角的内部平分线上的点到这个角的两边的距离相等.如图2.5所示,射线OC 是∠AOB 的平分线,则 DE=DF. 角平分线性质定理2 在△ABC中,AD 是∠BAC 的平分线,则有 (图2.6). 针对定理2的证明: 证法 1 如图2.7所示,过点 D作DF⊥AB,DG⊥AC.根据角平分线性质得 DF=DG,易得 整理得 证法 2 如图2.8所示,过点 C作CE∥AD交BA 延长线于点E. 因为 CE∥AD,所以∠1=∠E,∠2=∠3. 又 AD 平分∠BAC,则∠1=∠2,故∠E=∠3,则AE=AC. 由 CE∥AD 可得 故 解题原理 对于全等型的角平分线题型,本质原理是“遇角分,作对称”即可,常见的对称图形如图2.9所示(虚线部分在做题时需要补形). 特别地,当“角平分线”遇到“平行线”时,会产生等腰三角形,如图2.10所示,已知 OA平分∠BOC,AB∥OC,则△AOB 为等腰三角形. 常见倒角模型 1.三个倒角模型 (1) 双内模型(图2.11) 已知:点P 为两内角平分线交点. 结论: 证明:设∠ABP =∠CBP =α,∠ACP =∠BCP =β,则 消去α+β后得证. (2) 内外模型(图2.12) 已知:点P 为内、外角平分线交点. 结论: 证明:设∠ACP=∠DCP=α,∠ABP=∠DBP=β,则 消去β-α后得证. (3) 两外模型(图2.13) 已知:点P 为两外角平分线交点. 结论: 证明:设 连接AP,所以 消去α+β后得证. 2.二倍角的处理方式 如图2.14所示,∠ABC=2∠ACB. 思 路 1 利用角平分线(倍角化半角). 如图2.15所示,作∠ABC的平分线,此时△BCD 为等腰三角形. 思 路 2 利用小角等腰(倍角化半角). 如图2.16所示,延长CB 至点D,使 BD=BA,此时△ACD 为等腰三角形. 思 路 3 利用大角等腰(半角化倍角). 如图2.17所示,作∠DBC=∠DCB,此时△BCD为等腰三角形且∠DCA=∠BCA. 思路 4 利用大角等腰(半角化倍角). 如图2.18所示,作 AC 的中垂线,交 BC 于点D,此时△ABD 为等腰三角形. 思 路 5 利用整体翻折(半角化倍角). 如图2.19所示,将△ABC 沿着BC 的中垂线翻折,此时四边形 ABCD 为等腰梯形,倒角后可得△ACD 为等腰三角形. 实例剖析 如图 2.20 所示,在△ABC 中,∠ABC =2∠ACB.若 AB = 3,BC = 5,则 AC = 【答案】 2 【分析】 思路 1 利用角平分线. 如图2.21所示,作∠ABC 的平分线,此时△BCD 为等腰三角形,根据角平分线第二定理可得 设 AD=3a,则 DC=5a,易证 △ABD∽△ACB,所以 AC,即9=3a·8a,解得 则 思路 2 利用小角等腰. 如图2.22所示,延长CB至点D,使 BD=BA,此时△ACD 为等腰三角形,作 AE⊥CD于点 E,易得 BE = 1,CE = 4,利用勾股定理得. 在 Rt△AEC 中, AC = 思路 3 利用大角等腰. 如图2.23所示,作AE⊥BC 于点E,在 BC上取点D,使AD=AB,此时△ACD为等腰三角形,易得 BE= ED =1,CD =3,利用勾股定理得 在 Rt△AEC 中,AC= 思路 4 整体对称法. 中小学教育资源及组卷应用平台 如图2.24所示,将△ABC 沿着BC 的中垂线翻折,此时四边形 ABCD 为等腰梯形,作AE⊥BC 于点E,易得 利用勾股定理得 在Rt△AEC中, 模块2 场 景 演 练 模型的识别:角平分线性质定理1 类型1:垂两边,全等现 1. 如图2.25所示,AB∥CD,O为∠BAC,∠ACD的平分线的交点,OE⊥AC于点E,若两平行线间的距离为6,则OE= . 类型2:垂角分,等腰成 2. 如图2.26所示,在 中,BD 平分 ,过点 C 作( 于点D,E 是边AC 的中点,连接DE.若, ,则 AB的长为 . 3. 如图2.27所示,在 中, BE 平分 求证: 4. 如图2.2 ... ...
~~ 您好,已阅读到文档的结尾了 ~~