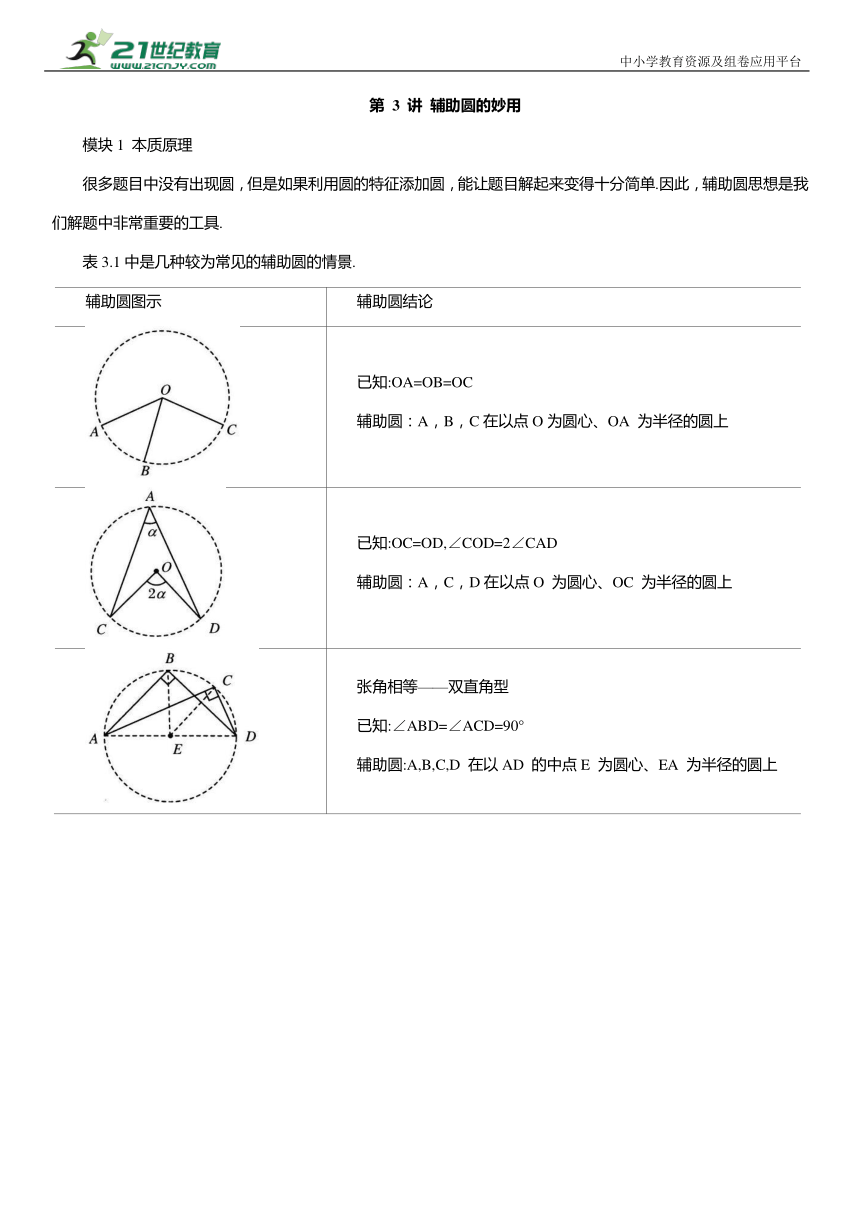
第 3 讲 辅助圆的妙用 模块1 本质原理 很多题目中没有出现圆,但是如果利用圆的特征添加圆,能让题目解起来变得十分简单.因此,辅助圆思想是我们解题中非常重要的工具. 表3.1中是几种较为常见的辅助圆的情景. 辅助圆图示 辅助圆结论 已知:OA=OB=OC 辅助圆:A,B,C在以点O为圆心、OA 为半径的圆上 已知:OC=OD,∠COD=2∠CAD 辅助圆:A,C,D在以点O 为圆心、OC 为半径的圆上 张角相等———双直角型 已知:∠ABD=∠ACD=90° 辅助圆:A,B,C,D 在以AD 的中点E 为圆心、EA 为半径的圆上 中小学教育资源及组卷应用平台 续表 辅助圆图示 辅助圆结论 张角相等———双锐角型 已知:∠ADB=∠ACB 辅助圆:A,B,C,D在同一圆上 对角互补型———双直角型 已知:∠ABC=∠ADC=90° 辅助圆:A,B,C,D 在以AC 的中点E 为圆心、EA 为半径的圆上 对角互补型 已知:∠ABC+∠ADC=180° 辅助圆:A,B,C,D在同一圆上 辅助圆的本质原理就是:锁定圆的轨迹,利用圆的性质与定理,确定边角关系. 辅助圆的惯用性质、定理如下: (1) 等量关系定理(图3.1) 在同圆或等圆中,等圆心角(∠AOB=∠DOC)、等弧 等弦(AB=CD)、等弦心距(OF=OG),知一推三;求证的核心是:△AOB≌△COD. (2) 垂径定理(图3.2) 垂径定理中的五个条件:过圆心的线(AB)、垂直弦(AB⊥CD)、平分弦(CE=DE)、平分优弧 平分劣弧 知二推三;求证的核心是: (3)圆周角定理及其推论 ①同弧所对的圆周角等于它所对的圆心角的一半(如图3.3所示, 2∠D=2∠E). ② 同弧或等弧所对的圆周角相等(如图3.3所示, ③ 直径所对的圆周角是直角(如图3.4所示, ④ 圆内接四边形对角互补,外角等于内对角(如图3.5所示, 进而∠A=∠1). (4)圆幂定理 ① 相交弦定理(图3.6). 结论: 证明提示: ② 切割线定理(PA 为切线)(图3.7). 结论: 证明提示:△PAC∽△PDA. ③割线定理(图3.8). 结论:PA·PB=PC·PD. 证明提示:△PBC∽△PDA. 模块2 场 景 演 练 四点共圆的判定 类型1:双垂直型 1. 如图3.9所示,AB 是⊙O的直径,CD 是弦,且 于点K. E为劣弧 上的一点,连接 AE 交DC 的延长线于点F.求证:E,F,B,K 四点共圆. 类型2:双锐角型 2. 如图3.10所示,四边形 ABCD 内接于⊙O,P,Q,R 分别是AB,BC,AD的中点.连接QP 与DA 的延长线交于点S,连接RP 与CB 的延长线交于点T.求证:S,T,Q,R 四点共圆. 类型3:对角互补型 3. 如图3.11所示,P为 内一点,D,E,F分别在BC,CA,AB边上,已知 P,D,C,E四点共圆,P,E,A,F四点共圆.求证:B,D,P,F也四点共圆. 辅助圆的应用:计算与证明 4. 如图3.12 所示,在四边形 ABCD 中,, 若 则 5.如图3.13 所示,正方形 ABCD 的中心为O,面积为 ,P为正方形内一点,且 则 6. 如图3.14所示,平面上有四个点 A,O,B,C,其中∠AOB=120°,∠ACB=60°,AO 则 7. 如图3.15所示,在 中, 点 P 为 外一点(P与C在直线AB 异侧),且 .设点 P 关于AB 的对称点为E,连接 PE,CE,线段 AB与CE 的数量关系为 . 8. 如图3.16所示,已知四边形 ABCD, 且 b,则 9. 如图3.17所示,四边形 ABCD 是正方形,M 是BC 上一点, 交 的外角平分线于点E.求证: 10. 如图3.18所示,已知 是等腰三角形, 点 D 在BC 上(不与BC 的中点重合),连接AD.作点C 关于AD 的对称点E,连接EB并延长交AD的延长线于点 F,连接AE,DE. (1) 证明:A,D,B,E四点共圆. (2)AD·AF的值是否会发生变化 若不变化,求出其值;若变化,请说明理由. 辅助圆的应用:定弦定角 如图3.19所示,在△ABC中,AB 的长为定值(即 AB=a),∠C 的角度为定值(即∠C=α),该图形为定弦定角模型. 情景 1 如图3.20所示,当∠C<90°时,点 C 在△ABC 外接圆⊙O 的优弧 上运动(不与点 A,B重合).此时,OA=OB=OC,∠AOB=2∠ACB. 情 景 2 如图3.21所示,当∠C=90°时,点 C 在△ABC 外接圆⊙O 上运动(不与点A,B重合).此时,OA=OB=OC. 情景 3 ... ...
~~ 您好,已阅读到文档的结尾了 ~~

