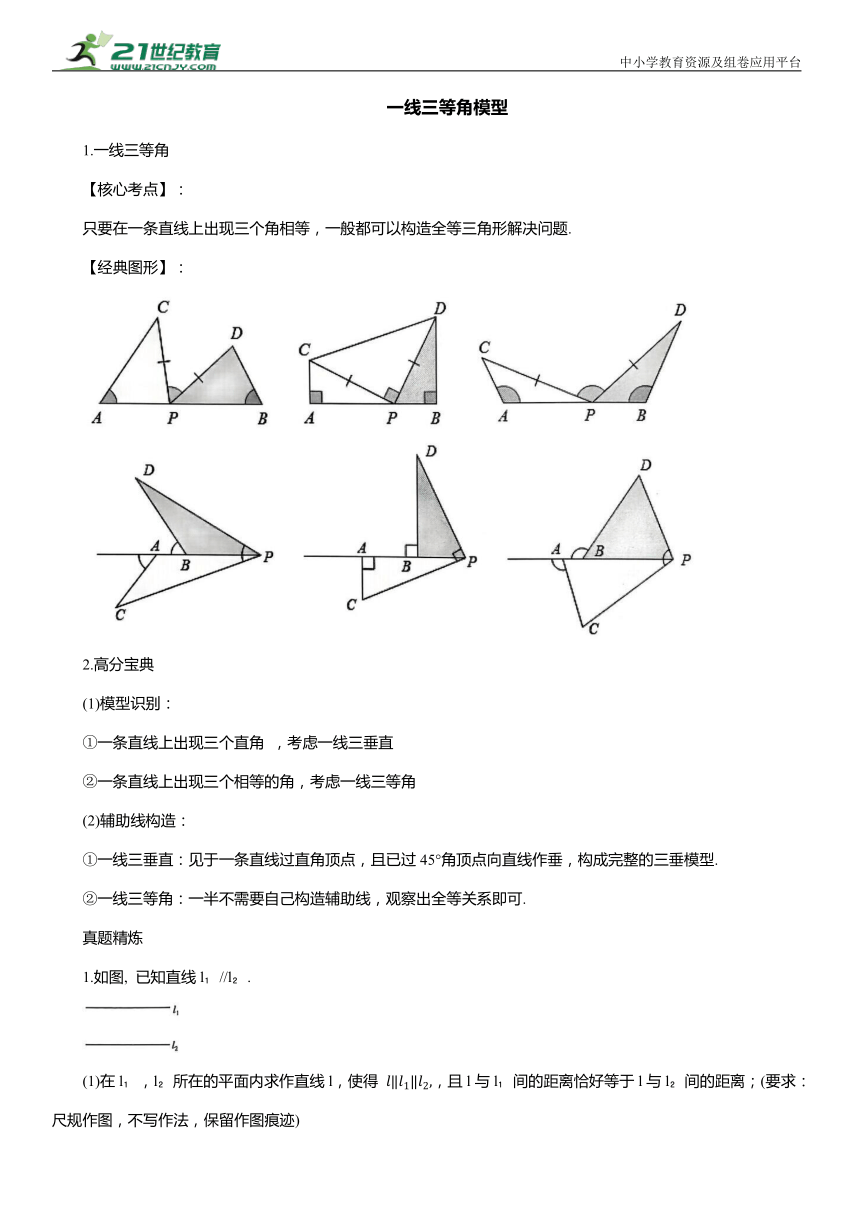
一线三等角模型 1.一线三等角 【核心考点】: 只要在一条直线上出现三个角相等,一般都可以构造全等三角形解决问题. 【经典图形】: 2.高分宝典 (1)模型识别: ①一条直线上出现三个直角 ,考虑一线三垂直 ②一条直线上出现三个相等的角,考虑一线三等角 (2)辅助线构造: ①一线三垂直:见于一条直线过直角顶点,且已过45°角顶点向直线作垂,构成完整的三垂模型. ②一线三等角:一半不需要自己构造辅助线,观察出全等关系即可. 真题精炼 1.如图, 已知直线l //l . (1)在l ,l 所在的平面内求作直线l,使得 ,且l与l 间的距离恰好等于l与l 间的距离;(要求:尺规作图,不写作法,保留作图痕迹) (2) 在(1) 的条件下, 若l 与l 间的距离为2,点A, B, C分别在l, 上,且 为等腰直角三角形,求△ABC的面积. 2【模型建立】 (1)如图1, 已知△ABE和△BCD,AB⊥BC,AB=BC,CD⊥BD, AE⊥BD .用等式写出线段AE ,DE,CD的数量关系,并说明理由. 【模型应用】 (2)如图2,在正方形ABCD中,点E,F分别在对角线BD和边CD上,. , 用等式写出线段BE,AD,DF的数量关系,并说明理由. 【模型迁移】 (3)如图3,在正方形ABCD中,点E在对角线BD上,点F在边CD的延长线上, .用等式写出线段BE,AD,DF的数量关系,并说明理由. 3如图,在Rt△ABC中,∠ACB=90°, AC= BC=5 .正方形DEFG的边长为 ,它的顶点D, E, G分别在△ABC的边上, 则BG的长为 4如图边长为6的等边△ABC,AD与BE交于点P, 若BD=CE=2, 则△ABP周长为 . 5如图边长为4的正方形ABCD,点E , F在CD,AC上, BF⊥EF,CE=1, 则AF长是( ) 6如图,正比例函数y=x的图象与反比例函数 的图象交于点A(1,a), 在△ABC中,∠ACB=90°,CA=CB,点C坐标为(-2,0). (1) 求k的值. (2)求AB所在直线的解析式. 7如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上, OA=2, 将△AOB绕点O逆时针旋转90°, 点B的对应点B'的坐标是( ) 8在平面直角坐标系xOy中,矩形OABC的点A在函数 的图象上,点C在函数 的图象上,若点B的横坐标为 则点A的坐标为( ) 9如图A(2,0), B(0,1), AC由AB绕点A顺时针旋转90°而得, 则AC所在直线解析式是 10正方形和等腰Rt△AEF, AB=5,AE=4.△AEF绕A转,∠ ABF最大, 11如图.已知点A(4,3),点B为直线y =-2上的一动点,点C(0,n),-2
~~ 您好,已阅读到文档的结尾了 ~~