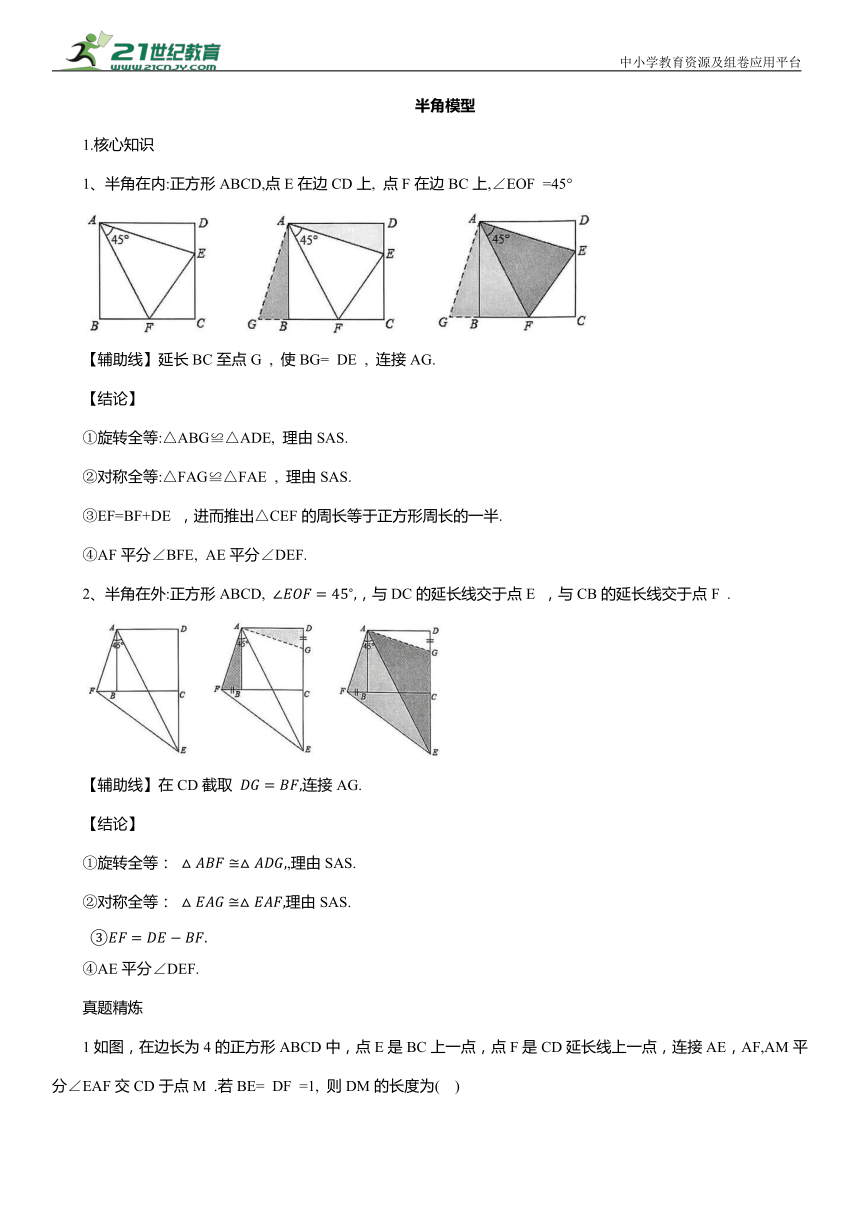
半角模型 1.核心知识 1、半角在内:正方形ABCD,点E在边CD上, 点F在边BC上,∠EOF =45° 【辅助线】延长BC至点G , 使BG= DE , 连接AG. 【结论】 ①旋转全等:△ABG≌△ADE, 理由SAS. ②对称全等:△FAG≌△FAE , 理由SAS. ③EF=BF+DE ,进而推出△CEF的周长等于正方形周长的一半. ④AF平分∠BFE, AE平分∠DEF. 2、半角在外:正方形ABCD, ,与DC的延长线交于点E ,与CB的延长线交于点F . 【辅助线】在CD截取 连接AG. 【结论】 ①旋转全等: ,理由SAS. ②对称全等: 理由SAS. ④AE平分∠DEF. 真题精炼 1如图,在边长为4的正方形ABCD中,点E是BC上一点,点F是CD延长线上一点,连接AE,AF,AM平分∠EAF交CD于点M .若BE= DF =1, 则DM的长度为( ) A.2 2正方形ABCD中,点E在边BC ,CD上运动(不与正方形顶点重合).作射线AE,将射线AE绕点A逆时针旋转45°,交射线CD于点F . (1)如图,点E在边BC上,BE =DF ,则图中与线段AE相等的线段是 (2) 过点E作EG⊥AF, 垂足为G, 连接DG, 求∠GDC的度数. 3在复习课上,刘老师先引导学生解决以下问题: 【问题情境】如图1,在△ABC中,∠BAC=90°,AB= AC,点D、E在边BC上,且∠DAE=45°,BD=3,CE=4,求DE的长.解:如图2, 将△ABD绕点A逆时针旋转90°得到△ACD', 连结ED' . 由旋转的特征得∠BAD=∠CAD',∠B=∠ACD', AD= AD',BD=CD'.∵∠BAC=90°,∠DAE=45°,∴∠BAD+∠EAC=45°.∵∠BAD=∠CAD',∴∠CAD'+∠EAC=45°,即∠EAD'=45°.∴∠DAE=∠D'AE.在△DAE和 中, ∠DAE=∠D'AE, AE=AE,∴ ① .∴DE=D'E .又∵ ∠ECD'=∠ECA+∠ACD'=∠ECA+∠B=90°,∴在Rt△ECD'中, ② . ∵CD'=BD=3,CE=4, 【问题解决】上述问题情境中, “①”处应填: ; “②”处应填: ; “③”处应填: .刘老师进一步谈到:图形的变化强调从运动变化的观点来研究,只要我们抓住了变化中的不变量,就能以不变应万变. 【知识迁移】如图3,在正方形ABCD中,点E、F分别在边BC、 CD上,满足△CEF的周长等于正方形ABCD的周长的一半,连结AE、 AF,分别与对角线BD交于M、N两点.探究BM、MN、 DN的数量关系并证明. 【拓展应用】如图4,在矩形ABCD中,点E、F分别在边BC、 CD上,且∠EAF=∠CEF=45°.探究BE、EF、 DF的数量关系: 【问题再探】如图5,在△ABC中,∠ABC=90°,AB=4,BC=3,点D、E在边AC上,且∠DBE=45°.设AD=x,CE=y,求y与x的函数关系式. 4(1)操作一:如图①,已知正方形纸片ABCD,将正方形纸片沿过点A的直线折叠,使点B落在正方形ABCD的内部,点B的对应点为点M,折痕为AE,再将纸片沿过点A的直线折叠,使AD与AM重合,折痕为AF,则 度. (2)操作二:如图②,将正方形纸片沿EF继续折叠,点C的对应点为点N .我们发现,当点E的位置不同时,点N的位置也不同.当点E在BC边的某一位置时,点N恰好落在折痕AE上,则 度. (3)在图②中,运用以上操作所得结论,解答下列问题: ① 设AM与NF的交点为点P .求证: ② 若 则线段AP的长为 . 5数学实践活动 ,是一种非常有效的学习方式. 折一折:将正方形纸片ABCD折叠,使边AB、AD都落在对角线AC上,展开得折痕AE、AF,连接EF ,如图1. ,写出图中两个等腰三角形 : (不需要添加字母); 转一转:将图1中的 绕点A旋转,使它的两边分别交边BC、CD于点P、Q,连接PQ,如图2. (2) 线段BP、PQ、DQ之间的数量关系为 . (3)连接正方形对角线BD ,若图2中的. 的边AP、AQ分别交对角线BD于点M、点N,如图3,则 剪一剪:将图3中的正方形纸片沿对角线BD剪开,如图4. (4) 求证 : 6如图,在正方形ABCD中,点O是对角线BD的中点,点P在线段OD上,连接AP并延长交CD于点E,过点P作 交BC于点F ,连接AF、EF , AF交BD于G, 现有以下结论:①AP =PF;②DE+BF=EF;③PB--PD= BF ;④S△AEF为定值;⑤S四边形PEFG = S△APG .以上结论正确的有 (填入正确的序号即可) ... ...
~~ 您好,已阅读到文档的结尾了 ~~

