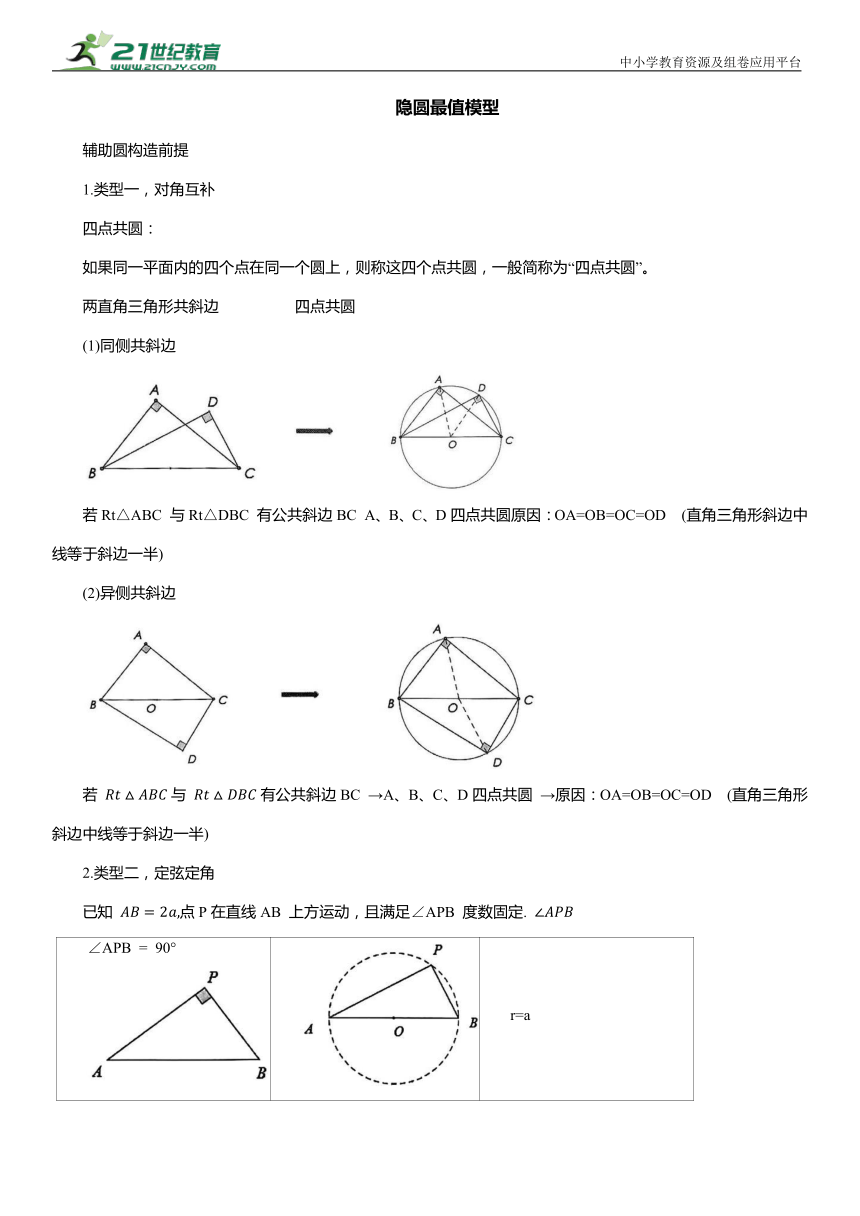
隐圆最值模型 辅助圆构造前提 1.类型一,对角互补 四点共圆: 如果同一平面内的四个点在同一个圆上,则称这四个点共圆,一般简称为“四点共圆”。 两直角三角形共斜边 四点共圆 (1)同侧共斜边 若Rt△ABC 与Rt△DBC 有公共斜边BC A、B、C、D四点共圆原因:OA=OB=OC=OD (直角三角形斜边中线等于斜边一半) (2)异侧共斜边 若 与 有公共斜边BC →A、B、C、D四点共圆 →原因:OA=OB=OC=OD (直角三角形斜边中线等于斜边一半) 2.类型二,定弦定角 已知 点P在直线AB 上方运动,且满足∠APB 度数固定. ∠APB = 90° r=a ∠APB=60° r=2 ∠APB=120° 3.类型三,定点定长 三条等线段共顶点,则三点共圆,公共点为圆心. 若OA=OB=OC A、B、C在以O为圆心的圆上 品真题精炼 1矩形+动点+对角线+定弦定直角———24苏州+选择压轴+初三 如图,矩形ABCD中, 动点E,F分别从点A ,C同时出发,以每秒1个单位长度的速度沿AB,CD向终点B,D运动,过点E,F作直线l,过点A作直线l的垂线,垂足为G,则AG的最大值为 ( ) A. C. 2 D. 1 2.等腰直角三角形+旋转+定点定长+定弦定直角———24河南+填空压轴+初三 如图,在Rt△ABC中,∠ACB=90°,CA=CB=3,线段CD绕点C在平面内旋转,过点B作AD的垂线,交射线AD于点E.若CD =1,则AE的最大值为 ,最小值为 3.等腰直角三角形+定长定角———24达州+选择压轴+初三 如图,△ABC是等腰直角三角形,∠ABC=90°, AB=4,点D , E分别在AC, BC边上运动,连接AE,BD交于点F ,且始终满足 则下列结论: ①AED= ②∠DFE=135°; ③△ABF的面积的最大值是;( ④CF|的最小值是 其中正确的是( ) A. ①③ B. ①②④ C. ②③④ D. ①②③④ 4.等腰三角形+定点定长+对称+面积最值———23淮安+填空压轴+初三 在四边形ABCD中, BH为∠ABC内部的任意一条射线( ∠CBH不等于( 点C关于BH的对称点为( 直线 与BH交于点F , 连接CC'、CF , 则 的面积的最大值是 5.等腰直角三角形+定点定长+点圆最值———23徐州+填空压轴+初三 如图 ,D在边BC上.△ACD沿AD折叠, 点C落在点C'处, 连接 ,,则 的最小值为 6定弦定直角+点圆最值———23菏泽+填空压轴+初三 如图,在四边形ABCD中,∠ ,点E在线段BC上运动,点F在线段AE上,. ,则线段BF的最小值为 7.矩形+中点+动点+对角线+定长定直角———22宿迁+填空压轴+初三 如图矩形ABCD, 点M、N是边AD、BC中点,某一时刻,动点E从点M出发,沿MA方向以每秒2个单位长度的速度向点A匀速运动;同时,动点F从点N出发,沿NC方向以每秒1个单位长度的速度向点C匀速运动,其中一点运动到矩形顶点时,两点同时停止运动,连接EF ,过点B作EF的垂线,垂足为H .在这一过程中,点H所经过的路径长是 8.圆+特殊角度+对角互补+面积最值———22苏州模拟+填空压轴+初三 已知⊙O半径是2 ,M、N是⊙O上两个动点,且在直线l异侧,若 =45°, 则四边形MANB面积的最大值是 9.直角三角形+定长定直角+点圆最值———21广西+选择压轴+初三 如图,在△ABC中,∠ABC=90°, AB=8, BC=12, D为AC边上的一个动点, 连接BD, E为BD上的一个动点 ,连接AE,CE,当 E时,线段AE的最小值是 ( ) A. 3 B. 4 C. 5 D.6 10.直角三角形+勾股定理+定长定直角+点圆最值———21鄂州+选择压轴+初三 如图,在Rt△ABC中,. .点P为△ABC内一点,且满足 当PB的长度最小时,△ACP的面积是( ). A.3 11矩形+对称+定点定长+点圆最值———21攀枝花+选择压轴+初三 如图,在矩形ABCD中,已知 ,点P是BC边上一动点(点P不与B,C重合),连接AP,作点B关于直线AP的对称点M,则线段MC的最小值为( ) A. 2 C. 3 12.等边三角形+全等三角形+定长定角+点圆最值———21达州+填空压轴+初三 如图,在边长为6的等边. 中,点E ,F分别是边AC ,BC上的动点,且 连接BE, AF交于点P , 连接CP, 则CP的最小值为 . 1 ... ...
~~ 您好,已阅读到文档的结尾了 ~~