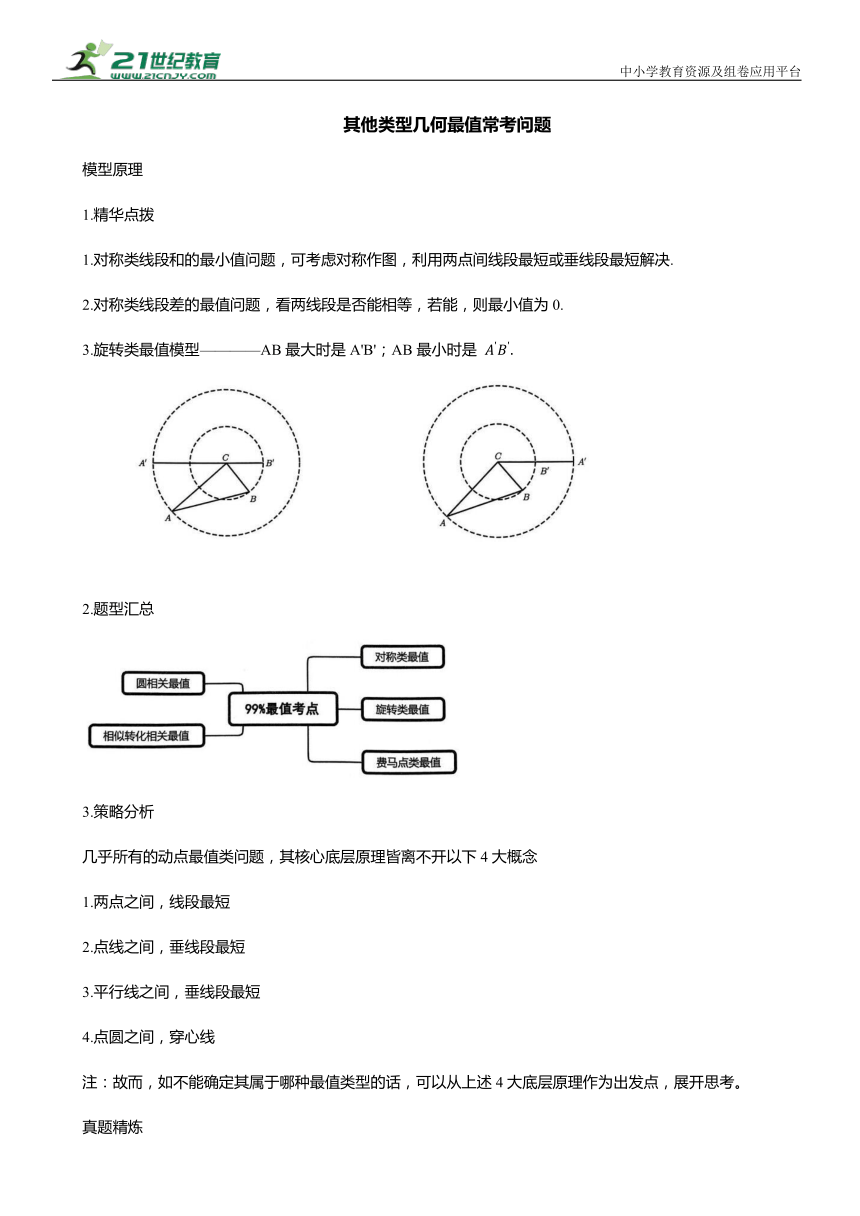
中小学教育资源及组卷应用平台 其他类型几何最值常考问题 模型原理 1.精华点拨 1.对称类线段和的最小值问题,可考虑对称作图,利用两点间线段最短或垂线段最短解决. 2.对称类线段差的最值问题,看两线段是否能相等,若能,则最小值为0. 3.旋转类最值模型———AB最大时是A'B';AB最小时是 2.题型汇总 3.策略分析 几乎所有的动点最值类问题,其核心底层原理皆离不开以下4大概念 1.两点之间,线段最短 2.点线之间,垂线段最短 3.平行线之间,垂线段最短 4.点圆之间,穿心线 注:故而,如不能确定其属于哪种最值类型的话,可以从上述4大底层原理作为出发点,展开思考。 真题精炼 1如图,在平面直角坐标系中,点A在直线 上,且点A的横坐标为4 ,直角三角板的直角顶点C.落在x轴上,一条直角边经过点A ,另一条直角边与直线OA交于点B ,当点C在x轴上移动时,线段AB的最小值为 . 2.如图平行线l 、l ,点A是l 上的定点,AB⊥l 于点B,点C、D分别是动点,且满足 BH⊥CD于点H ,则当∠BAH最大时, sin∠BAH的值为 3.如图,在边长为6的正方形ABCD中,点E ,F分别是边AB ,BC上的动点,且满足 点M是DF的中点, G是边AB上的点, AG =2GB,则 的最小值是( ) A.4 B. 5 C. 8 D. 10 4.如图, ⊙M的圆心为M(4,0), 半径为2, P是直线 上的一个动点,过点P作⊙M的切线,切点为Q,则PQ的最小值为 . 5.如图,在菱形ABCD中, E是BC边上一个动点,连接AE,AE的垂直平分线MN交AE于点M ,交BD于点N .连接EN,CN. (1)求证: (2)求 的最小值. 6.边长为2的等边 的A、 B在射线OM、ON上滑动, 若 ,则OC最大值是 7.如图,矩形ABCD中,. 点P在对角线BD上,过点P作MN⊥BD,交边AD, BC于点M , N , 过点M作 交BD于点E,连接EN,BM, DN .下列结论:① ②四边形MBND的面积不变;③当AM:MD=1:2时, ④BM+MN+ND的最小值是20.其中所有正确结论的序号是 8.如图,在菱形ABCD中, .折叠该菱形,使点A落在边BC上的点M处,折痕分别与边AB,AD交于点E ,F .当点M与点B重合时,EF的长为 ;当点M的位置变化时,DF长的最大值为 . 9.如图,在平面直角坐标系xOy中,点A的坐标为(0,4),P是x轴上一动点,把线段PA绕点P顺时针旋转 得到线段PF,连接OF,则线段OF长的最小值是 . 10如图矩形ABCD中, .若点E是边AD上的一动点 ,过点E作EF⊥AC且分别交对角线AC ,直线BC于点O、F,则点E移动过程中,. 最小值为 11等腰三角形+锐角三角函数+旋转+最大值———23菏泽模拟/21镇江+填空压轴+初三如图等腰三角形ABC, 点P在边AC上运动(可与A,C重合),将线段BP绕点P逆时针旋转120°,得到DP ,连接BD,则BD长最大值为 12.如图,在△ABC中,. ,点D、F分别在BC、AC上,( ,BF交AD于点E,则△AFE面积的最大值是 . 13.如图,矩形ABCD, 点A在x轴正半轴上,点D在y轴正半轴上.当点A在x轴上运动时,点D也随之在y轴上运动,在这个运动过程中,点C到原点O的最大距离为 . 14.如图,在△ABC中,∠ACB=90°,AC= BC=4,点D是BC边的中点,点P是AC边上一个动点,连接PD,以PD为边在PD的下方作等边三角形PDQ ,连接CQ,则CQ的最小值是( ) B. 1 15.如图,在△ACD中, ,且△DAB∽△DCA,若AD=3AP,点Q是线段AB上的动点, 则PQ的最小值是( ) 16.如图,等边三角形ABC的边长为4,⊙C的半径为 P为AB边上一动点,过点P作⊙C的切线PQ ,切点为Q ,则PQ的最小值为 17如图,在 中, ,D是BC的中点,直线l经过点D, 垂足分别为E ,F ,则AE+BF的最大值为( ) 18.等边三角形+旋转+全等+共线+最大最小值———221深圳模拟/20十堰+填空压轴+初三如图D是等边三角形ABC外一点 ,若 ,则AD最大值与最小值的差为 1如图,在平面直角坐标系中,点A在直线y= 上,且点A的横坐标为4,直角三角板的直角顶点C落在 ax轴上,一条直角边经过点A,另一条直角边与直线OA交于点B ,当点O ... ...
~~ 您好,已阅读到文档的结尾了 ~~