浙江省七彩阳光2024-2025学年高二（下）期中联考数学试卷(pdf版,含答案)

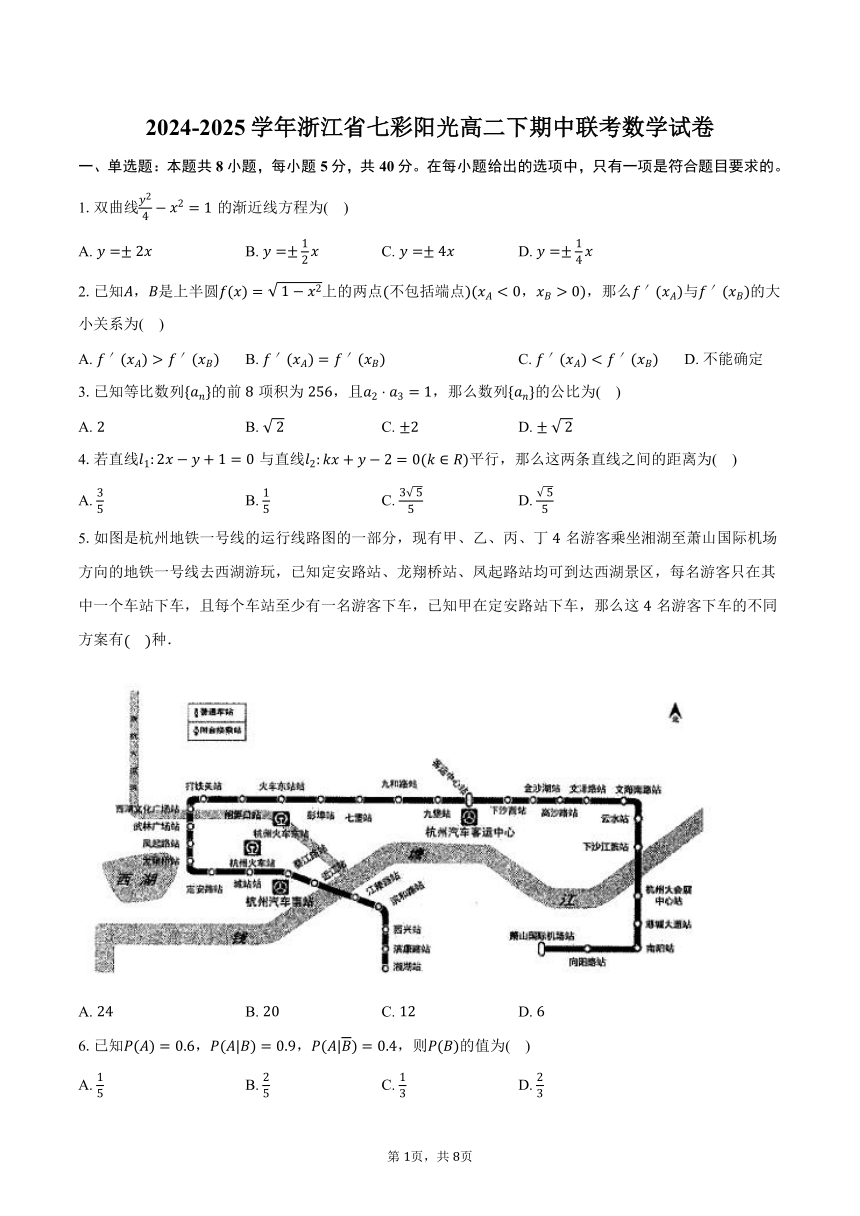
2024-2025 学年浙江省七彩阳光高二下期中联考数学试卷 一、单选题：本题共 8 小题，每小题 5 分，共 40 分。在每小题给出的选项中，只有一项是符合题目要求的。 2 1 .双曲线 24 = 1 的渐近线方程为( ) A. =± 2 B. =± 12 C. =± 4 D. =± 1 4 2.已知 ， 是上半圆 ( ) = 1 2上的两点(不包括端点)( < 0， > 0)，那么 ′( )与 ′( )的大 小关系为( ) A. ′( ) > ′( ) B. ′( ) = ′( ) C. ′( ) < ′( ) D.不能确定 3.已知等比数列{ }的前 8 项积为 256，且 2 3 = 1，那么数列{ }的公比为( ) A. 2 B. 2 C. ±2 D. ± 2 4.若直线 1: 2 + 1 = 0 与直线 2: + 2 = 0( ∈ )平行，那么这两条直线之间的距离为( ) A. 3 B. 1 3 5 55 5 C. 5 D. 5 5.如图是杭州地铁一号线的运行线路图的一部分，现有甲、乙、丙、丁 4 名游客乘坐湘湖至萧山国际机场 方向的地铁一号线去西湖游玩，已知定安路站、龙翔桥站、凤起路站均可到达西湖景区，每名游客只在其 中一个车站下车，且每个车站至少有一名游客下车，已知甲在定安路站下车，那么这 4 名游客下车的不同 方案有( )种． A. 24 B. 20 C. 12 D. 6 6.已知 ( ) = 0.6， ( | ) = 0.9， ( | ) = 0.4，则 ( )的值为( ) A. 15 B. 2 1 2 5 C. 3 D. 3 第 1页，共 8页 7 2 1.已知数列{ }的通项公式为 = lg 2 +1 ( ∈ )，则使数列{ }的前 项和 满足 + 2 < 0 的 的( ) A.最小值为 49 B.最大值为 49 C.最小值为 50 D.最大值为 50 8.在正方体 1 1 2 1 1中， = = 2 ， 3 23 3 ，在平面 1上存在一点 ，使得 tan∠ = 4 ， 则点 的轨迹为( ) A.圆 B.椭圆 C.双曲线 D.抛物线 二、多选题：本题共 3 小题，共 18 分。在每小题给出的选项中，有多项符合题目要求。 9.下列说法正确的有( ) A.若平面 的法向量 = (1,2,3)， = (3,0, 1)，则点 ∈平面 B.若平面 的法向量 = (1,1,2)， = (0,3,0)，则点 到平面 6的距离为 2 C. 5若平面 ， 的法向量分别为 1 = (1,8,4)， 2 = (1,0,2)，则两平面的夹角的余弦值为 5 D.空间中三个点 (0,2,1)， (1,4, 1)， (2,6, 3)，则∠ 为钝角 10.(3 2 )2025 = 0 + 1 + 22 + + 20242024 + 20252025 ，则下列选项正确的有( ) A. = 320250 B. 0 1 2 1 1 1 4050 1 + 4 2 8 3 + 22025 2025 = 2 C. | 0| + | 1| + | 2| + + | 2025| = 1 D. 0 + 2 1 + 3 2 + + 2026 2025 = 4049 11.设实数 > 0，若不等式 1 ≥ ln + 1 对任意 > 0 恒成立，那么 的取值可能是( ) A. 1 B. 1 2 C. D. 2 三、填空题：本题共 3 小题，每小题 5 分，共 15 分。 12.已知抛物线 : 2 = 4 的焦点为 ，点 ( , )在抛物线 上，若| | = 3，则 = ． 13.已知函数 ( ) = ( )2 3 + ln 在 = 1 处取得极大值， 则 = ． 14.将编号为 1，2，3，4 的四个小球随机放入编号为 1，2，3，4 的四个盒子中，要求每个小盒只能装一 个小球，用 表示编号与盒子编号相同的小球数，则 的分布列为 ． 四、解答题：本题共 5 小题，共 77 分。解答应写出文字说明，证明过程或演算步骤。 15.(本小题 13 分) 已知函数 ( ) = 1， ∈ (1)求 ( )在点(1, (1))处的切线方程; 第 2页，共 8页 1 (2) 2026比较 2025与2025的大小，并说明理由． 16.(本小题 15 分) : 2 2 3 已知椭圆 2 + 2 = 1( > > 0)的离心率为 2 ，椭圆的面积为 2 (1)求椭圆的标准方程; (2)已知直线 : = + 4与椭圆 相交于 ， 两点，且△ 的面积为5，求直线 的方程. (注：椭圆的面积 公式为 = ) 17.(本小题 15 分) 如图，四棱锥 的底面 为筝形， ⊥面 ，点 为 与 的交点，且 = = = = 12 (1)求证：面 ⊥面 ; (2) 1已知 为棱 上的一点，若 = 2 ，求二面角 的余弦值． (注：筝形是指有一条对角线所在直线为对称轴的四边形) 18.(本小题 17 分) 数列{ }满足 1 = 3，2 + +1 + 3 = 0． (1 ... ...