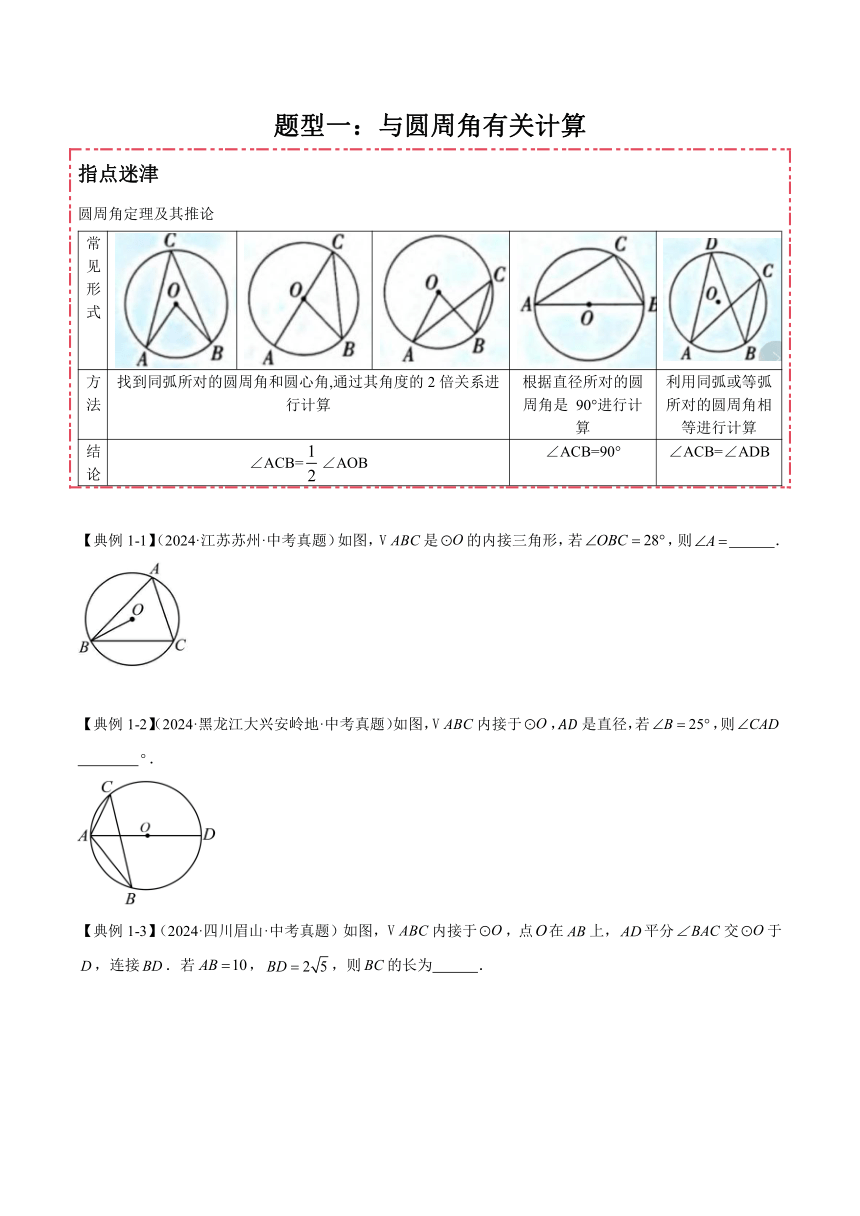
题型一:与圆周角有关计算 指点迷津 圆周角定理及其推论 常见形式方法找到同弧所对的圆周角和圆心角,通过其角度的2倍关系进行计算根据直径所对的圆周角是 90°进行计算利用同弧或等弧 所对的圆周角相等进行计算结论∠ACB=∠AOB∠ACB=90°∠ACB=∠ADB 【典例1-1】(2024·江苏苏州·中考真题)如图,是的内接三角形,若,则 . 【典例1-2】(2024·黑龙江大兴安岭地·中考真题)如图,内接于,是直径,若,则 . 【典例1-3】(2024·四川眉山·中考真题)如图,内接于,点在上,平分交于,连接.若,,则的长为 . 【典例1-4】(2024·陕西·中考真题)如图,是的弦,连接,,是所对的圆周角,则与的和的度数是 . 【典例1-5】(2024·山东泰安·中考真题)如图,是的直径,是的切线,点为上任意一点,点为的中点,连接交于点,延长与相交于点,若,,则的长为 . 【参考答案】 【典例1-1】【答案】/62度 【分析】本题考查了圆周角定理,等腰三角形的性质,三角形内角和定理,连接,利用等腰三角形的性质,三角形内角和定理求出的度数,然后利用圆周角定理求解即可. 【详解】解:连接, ∵,, ∴, ∴, ∴, 故答案为:. 【典例1-2】【答案】 【分析】本题考查了圆周角定理,直角三角形的两个锐角互余,连接,根据直径所对的圆周角是直角得出,根据同弧所对的圆周角相等得出,进而根据直角三角形的两个锐角互余,即可求解. 【详解】解:如图所示,连接, ∵内接于,是直径, ∴, ∵,, ∴ ∴, 故答案为:. 【典例1-3】【答案】 【分析】本题考查了圆周角定理,角平分线的定义全等三角形的判定和性质,勾股定理,相似三角形的判定和性质,延长,交于,由圆周角定理可得,,进而可证明,得到,即得,利用勾股定理得,再证明,得到,据此即可求解,正确作出辅助线是解题的关键. 【详解】解:延长,交于, 是的直径, ,, 平分, , 又∵, ∴, , , ,, , , 又∵, ∴, , , , , , 故答案为:. 【典例1-4】【答案】/90度 【分析】本题考查了圆周角定理,等腰三角形的性质,三角形内角和定理,熟练掌握圆周角定理是解题的关键.根据圆周角定理可得,结合三角形内角和定理,可证明,再根据等腰三角形的性质可知,由此即得答案. 【详解】是所对的圆周角,是所对的圆心角, , , , , , , , . 故答案为:. 【典例1-5】【答案】 【分析】本题主要考查相似三角形的判定和性质、切线的性质、圆周角定理等知识,熟练掌握相关知识是解题关键. 先证可得从而得到,求得,再运用勾股定理可得,再根据圆周角定理以及角的和差可得,最后根据等角对等边即可解答. 【详解】解:∵是的直径, ∴, ∵是的切线, ∴, ∴, ∴, ∴, ∵, ∴, ∴, ∵点为的中点, ∴, ∴, ∵, ∴,即, ∴. 故答案为:. ... ...
~~ 您好,已阅读到文档的结尾了 ~~