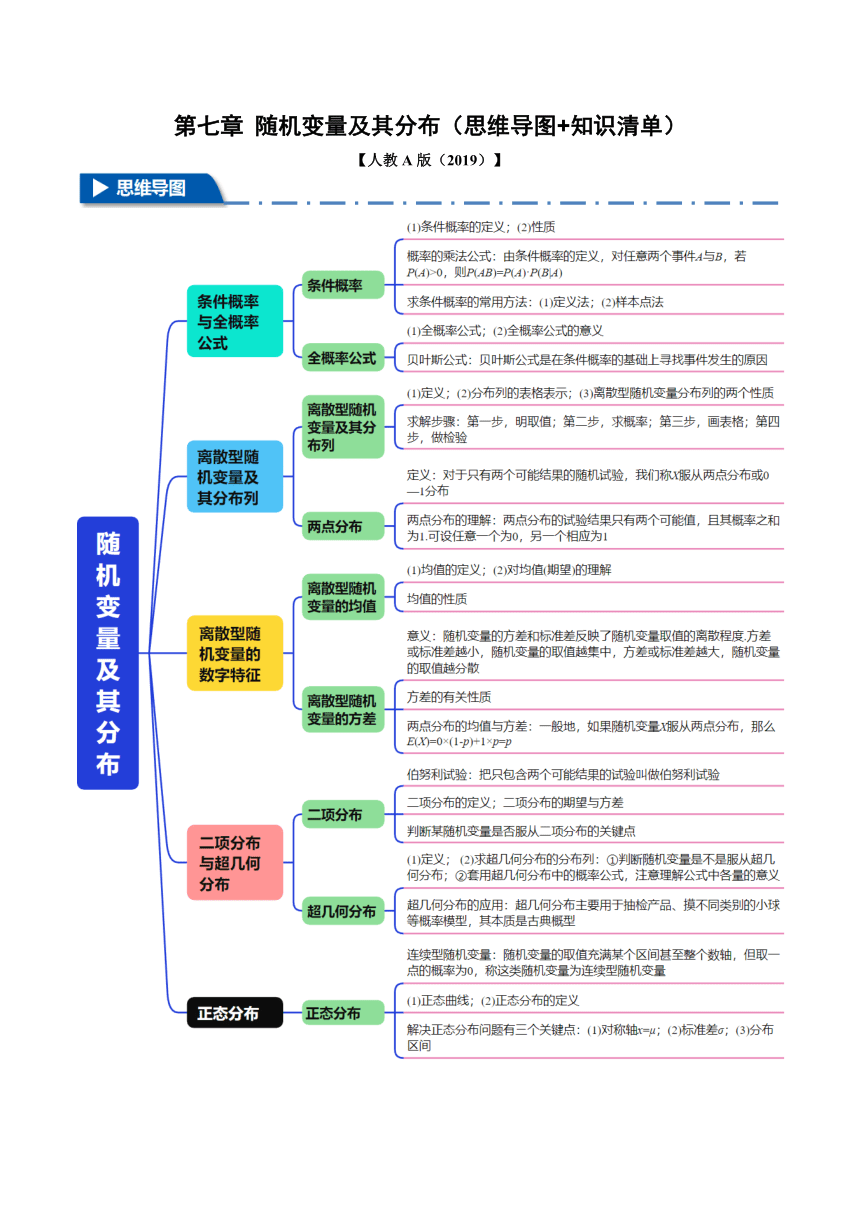
第七章 随机变量及其分布(思维导图+知识清单) 【人教 A 版(2019)】 7.1 条件概率与全概率公式 【知识点 1 条件概率】 1.条件概率 (1)条件概率的定义 一般地,设 A,B 为两个随机事件,且 P(A)>0,我们称 P(B|A)= 为事件 A 发生的条件下,事件 B 发生的条件概率,简称条件概率. (2)性质 设 P(A)>0,Ω 为样本空间,则 ①P(B|A)∈[0,1],P(Ω|A)=1; ②如果 B 和 C 是两个互斥事件,则 P(B∪C|A)=P(B|A)+P(C|A); ③设 和 B 互为对立事件,则 P( )=1-P(B|A). 2.概率的乘法公式 由条件概率的定义,对任意两个事件 A 与 B,若 P(A)>0,则 P(AB)=P(A)·P(B|A). 3.求条件概率的常用方法 (1)定义法:P(B|A)= . (2)样本点法:P(B|A)= . 【知识点 2 全概率公式】 1.全概率公式及应用 (1)全概率公式 一般地,设 是一组两两互斥的事件, =Ω,且 P(Ai)>0,i=1,2, , n,则对任意的事件 ,有 P(B)= .我们称此公式为全概率公式. (2)全概率公式的意义 全概率公式的意义在于,当直接计算事件 B 发生的概率 P(B)较为困难时,可以先找到样本空间 Ω 的一 个划分 Ω= , 两两互斥,将 看成是导致 B 发生的一组原 因,这样事件 B 就被分解成了 n 个部分,分别计算 P( ),P( ), ,P( ),再利用全概率公式求 解. 2.贝叶斯公式 设 是一组两两互斥的事件, =Ω,且 P(Ai)>0,i=1,2, ,n,则对 任意的事件 ,P(B)>0,有 . 贝叶斯公式是在条件概率的基础上寻找事件发生的原因,在运用贝叶斯公式时,一般已知和未知条件 如下: (1)A 的多种情况中到底哪种情况发生是未知的,但是每种情况发生的概率已知,即 P(Ai)已知; (2)事件 B 是已经发生的确定事实,且 A 的每种情况发生的条件下 B 发生的概率已知,即 P( )已知; (3)P(B)未知,需要使用全概率公式计算得到; (4)求解的目标是用 A 的某种情况 Ai的无条件概率求其在 B 发生的条件下的有条件概率 P( ). 3.利用全概率公式的解题思路 (1)按照确定的标准,将一个复合事件分解为若干个互斥事件 Ai(i=1,2,…,n); (2)求 P(Ai)和所求事件 B 在各个互斥事件 Ai发生条件下的概率 P(B|Ai); (3)代入全概率公式计算. 7.2 离散型随机变量及其分布列 【知识点 1 离散型随机变量及其分布列】 1.随机变量与离散型随机变量 (1)随机变量 ①定义:一般地,对于随机试验样本空间 Ω 中的每个样本点ω,都有唯一的实数 X(ω)与之对应,我们 称 X 为随机变量. ②表示:通常用大写英文字母表示随机变量,用小写英文字母表示随机变量的取值. ③随机变量与函数的关系 联系:随机变量与函数都是一种对应关系,样本点ω相当于函数定义中的自变量,样本空间 Ω 相当于 函数的定义域. 区别:样本空间 Ω 不一定是数集,随机变量的取值 X(ω)随着试验结果ω的变化而变化,而函数是从非 空数集到非空数集的一一对应. (2)离散型随机变量 可能取值为有限个或可以一一列举的随机变量,称为离散型随机变量. 2.离散型随机变量的分布列 (1)定义 一般地,设离散型随机变量 X 的可能取值为 x1,x2,…,xn,我们称 X 取每一个值 xi的概率 P(X=xi)= pi,i=1,2,…,n 为 X 的概率分布列,简称分布列. (2)分布列的表格表示 X x1 x2 xn P p1 p2 pn 分布列也可以用等式形式表示为 P(X=xi)=pi,i=1,2, ,n,还可以用图形表示. (3)离散型随机变量分布列具有的两个性质 ①pi≥0,i=1,2, ,n; ②p1+p2+ +pn=1. 3.离散型随机变量分布列的求解步骤 第一步,明取值:明确随机变量的可能取值有哪些,且每一个取值所表示的意义; 第二步,求概率:要弄清楚随机变量的概率类型,利用相关公式求出变量所对应的概率; 第三步,画表格:按规范要求形式写出分布列; 第四步,做检验:利用分布列的性质检验分布列是否正确. 【知识点 2 两 ... ...
~~ 您好,已阅读到文档的结尾了 ~~