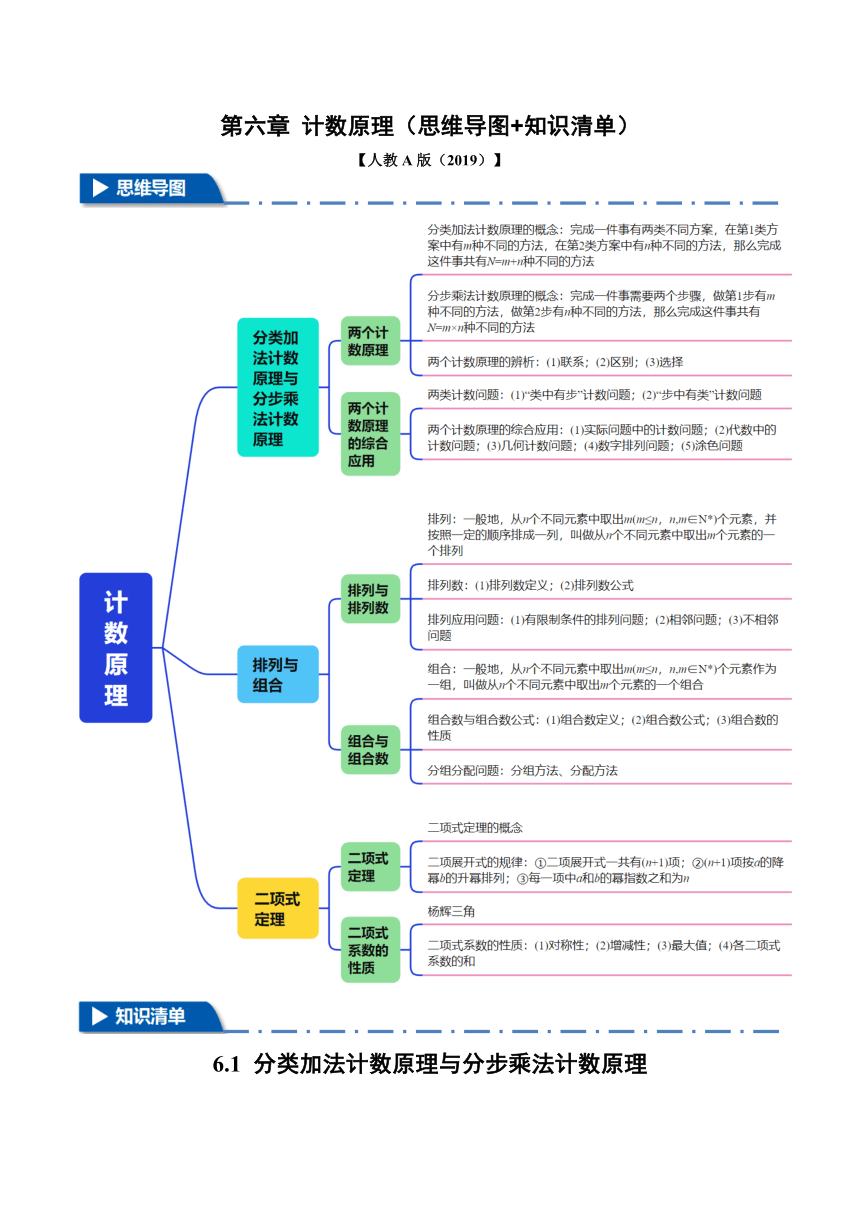
第六章 计数原理(思维导图+知识清单) 【人教 A 版(2019)】 6.1 分类加法计数原理与分步乘法计数原理 【知识点 1 分类加法计数原理与分步乘法计数原理】 1.分类加法计数原理 (1)分类加法计数原理的概念 完成一件事有两类不同方案,在第 1 类方案中有 m 种不同的方法,在第 2 类方案中有 n 种不同的方法, 那么完成这件事共有 N=m+n 种不同的方法. 概念推广:完成一件事有 n 类不同方案,在第 1 类方案中有 m1种不同的方法,在第 2 类方案中有 m2 种种不同的方法, ,在第 n 类方案中有 mn种种不同的方法,那么完成这件事共有 N= 种 不同的方法. (2)分类加法计数原理的特点 分类加法计数原理又称分类计数原理或加法原理,其特点是各类中的每一种方法都可以完成要做的事 情,我们可以用第一类有 m1种方法,第二类有 m2种方法, ,第 n 类有 mn种方法,来表示分类加法计 数原理,即强调每一类中的任一种方法都可以完成要做的事,因此一共有 种不同方法可 以完成这件事. (3)分类的原则 分类计数时,首先要根据问题的特点,确定一个适当的分类标准,然后利用这个分类标准进行分类, 分类时要注意两个基本原则:一是完成这件事的任何一种方法必须属于相应的类;二是不同类的任意两种 方法必须是不同的方法,只要满足这两个基本原则,就可以确保计数时不重不漏. 2.分步乘法计数原理 (1)分步乘法计数原理的概念 完成一件事需要两个步骤,做第 1 步有 m 种不同的方法,做第 2 步有 n 种不同的方法,那么完成这件 事共有 N=m×n 种不同的方法. 概念推广:完成一件事需要 n 个步骤,做第 1 步有 m1 种不同的方法,做第 2 步有 m2 种不同的方法, , 做第 n 步有 mn种不同的方法,那么完成这件事共有 N= 种不同的方法. (2)分步乘法计数原理的特点 分步乘法计数原理的特点是在所有的各步之中,每一步都要使用一种方法才能完成要做的事,可以利 用图形 来表示分步乘法计数原理,图中的“ ”强调要依次完成各个 步骤才能完成要做的事情,从而共有 种不同的方法可以完成这件事. (3)分步的原则 ①明确题目中所指的“完成一件事”是指什么事,怎样才能完成这件事,也就是说,弄清要经过哪几步才 能完成这件事; ②完成这件事需要分成若干个步骤,只有每个步骤都完成了,才算完成这件事,缺少任何一步,这件 事就不可能完成;不能缺少步骤. ③根据题意正确分步,要求各步之间必须连续,只有按照这 n 个步骤逐步去做,才能完成这件事,各 个步骤既不能重复也不能遗漏. 3.分类加法计数原理与分步乘法计数原理的辨析 (1)联系 分类加法计数原理和分步乘法计数原理解决的都是有关完成一件事的不同方法的种数问题. (2)区别 分类加法计数原理每次得到的都是最后结果,而分步乘法计数原理每步得到的都是中间结果,具体区 别如下表: 区别 分类加法计数原理 分步乘法计数原理 ① 针对的是“分类”问题 针对的是“分步”问题 ② 各种方法相互独立 各个步骤中的方法互相依存 用其中任何一种方法都可以完成这件 ③ 只有各个步骤都完成才算完成这件事 事 (3)分类加法计数原理与分步乘法计数原理的合理选择 分类→将问题分为互相排斥的几类,逐类解决→分类加法计数原理; 分步→将问题分为几个相互关联的步骤,逐步解决→分步乘法计数原理. 在解决有关计数问题时,应注意合理分类,准确分步,同时还要注意列举法、模型法、间接法和转换 法的应用. 【知识点 2 两个计数原理的综合应用】 1.两类计数问题的求解思路: (1)“类中有步”计数问题:完成一件事有几类方案,每一类方案中分若干步,利用分步乘法计数原 理求出每一类方案中的方法数,再利用分类加法计数原理把各类方案的方法数相加,即可得出结果. (2)“步中有类”计数问题:完成一件事的过程分成 ... ...
~~ 您好,已阅读到文档的结尾了 ~~