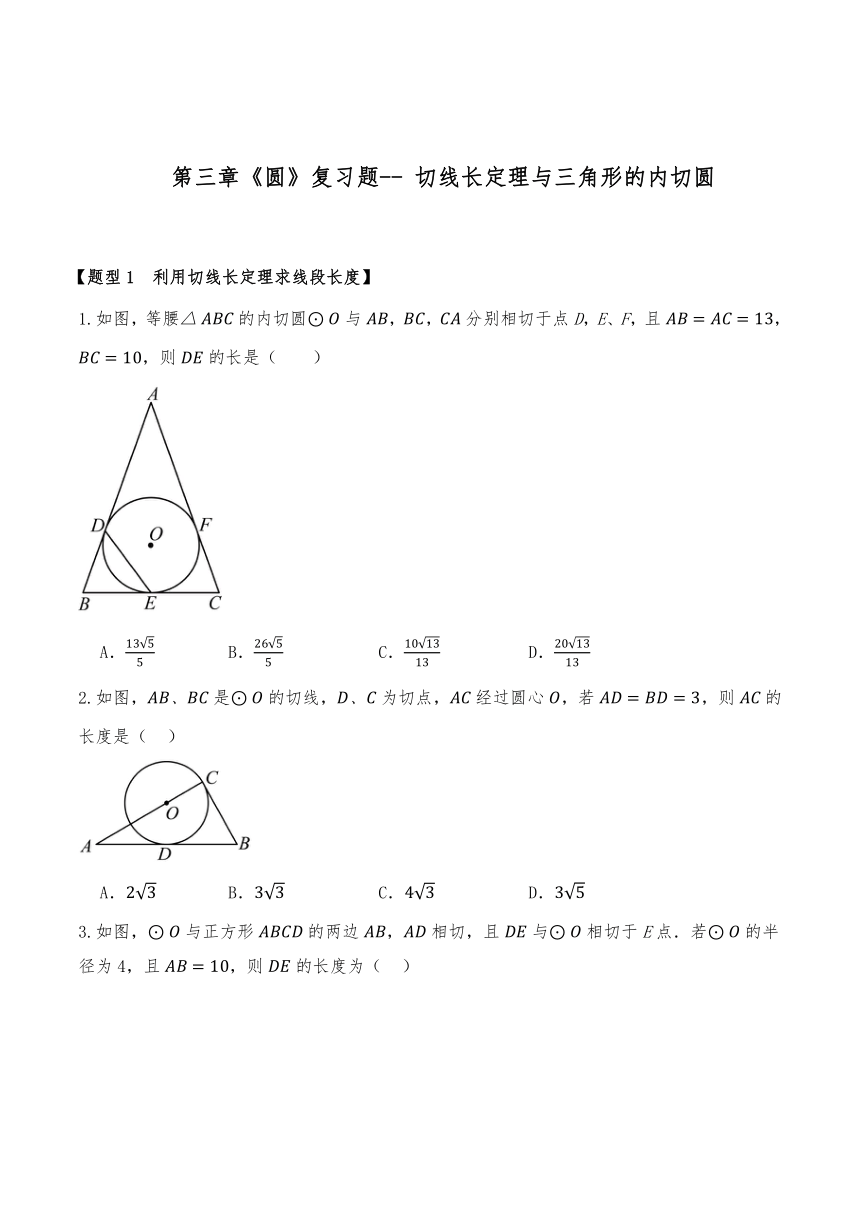
第三章《圆》复习题-- 切线长定理与三角形的内切圆 【题型1 利用切线长定理求线段长度】 1.如图,等腰的内切圆与,,分别相切于点D,E、F,且,,则的长是( ) A. B. C. D. 2.如图,是的切线,为切点,经过圆心,若,则的长度是( ) A. B. C. D. 3.如图,与正方形的两边,相切,且与相切于E点.若的半径为4,且,则的长度为( ) A.5 B.5.5 C. D.6 4.如图,为的直径,,分别与⊙O相切于点B,C,过点C作的垂线,垂足为E,交于点D.若,则长为( ) A.1 B.2 C.3 D.4 【题型2 利用切线长定理求周长】 1.如图,是的内切圆,分别与相切于D,E两点,已知,,则的周长为( ) A.14 B. C.16 D.18 2.如图,已知是边长为3的等边三角形,的半径为1,是上一动点,,分别切于点,,的另一条切线切于点,分别交,于点,.若是的中点,则的周长是( ) A. B.6 C. D. 3.如图,过点作的切线,,切点分别是,,连接.过上一点作的切线,交,于点,.若,的周长为4,则的长为( ) A.2 B. C.4 D. 4.已知是边长为3的等边三角形,的半径为是上一动点,分别切于点的另一条切线交于点,则周长的取值范围是( ) A. B. C. D. 【题型3 利用切线长定理求面积】 1.我们知道:过圆外一点所画的圆的两条切线长相等. 【问题解决】如图,现有一块边长为的正方形空地,在边取一点,以长为直径,在这个正方形的空地内建一个半圆形儿童游乐场,过点划出一条与这个半圆相切的分割线,正方形位于分割线右下方的部分作为娱乐区,娱乐区的最大面积等于( ) A. B. C. D. 2.如图,的内切圆分别与三边相切于点,点和点,若,,则的面积为 . 3.如图,直线分别与⊙相切于,且∥,连接,若,则梯形的面积等于( ) A.64 B.48 C.36 D.24 4.如图所示,在中,,以为直径的与边交于点,过点作的切线,交于点. (1)求证:. (2)若以,,,四点为顶点的四边形是正方形,的半径为,求的面积. (3)若,,求的半径的长. 【题型4 利用切线长定理求角度】 1.四边形是的外切四边形,若,则的度数是 . 2.如图,,是的两条切线,切点分别为,,连接,,若,则 °. 3.如图,是的切线,是切点,分别交于,两点,若,则 . 4.如图,A是外一点,分别与相切于点B,C.P是上任意一点,过点P作的切线,交于点M,交于点N.,则的周长是 ,若,则 . 【题型5 利用切线长定理进行证明】 1.如图,是的直径,,是的两条切线,切点分别为B,C.连接交于点D,交于点E,连接. (1)求证:; (2)若点E是的中点,的半径为6,求的长. 2.如图,,是的切线,,为切点,连接. (1)若与相切于点,求证; (2)若,求证与相切. 3.如图,在中,为直径,点M为延长线上的一点,与相切于点C,圆周上有另一点D与点C分居直径两侧,且使得,连接. 求证:①与相切; ②四边形是_____形; ③_____. 4.如图1所示,为的外接圆,为直径,、分别与相切于点D、C().E在线段上,连接并延长与直线相交于点P,B为中点. (1)证明:是的切线. (2)如图2,连接,,求证:. 【题型6 利用切线长定理求内切圆半径】 1.如图,在中,,,,则的内切圆半径 . 2.如图,将刻度尺、含角的直角三角板和量角器如图摆放(无重叠部分),若三角板角的顶点A在刻度尺上的读数是,量角器与刻度尺接触点在刻度尺上的读数是,量角器与三角板的接触点为B. (1) . (2)该量角器的直径长为 .(结果保留根号) 3.如图,在四边形中,分别与相切于B、E、A三点,为的直径.若,则的半径为 . 4.如图, 内切于正方形,边、上两点,,且是的切线,当的面积为时,则的半径是 . 【题型7 作三角形的内切圆】 1.如图,在的正方形网格中,有部分网格线被擦去.点,,在格点(正方形网格的交点)上. ... ...
~~ 您好,已阅读到文档的结尾了 ~~