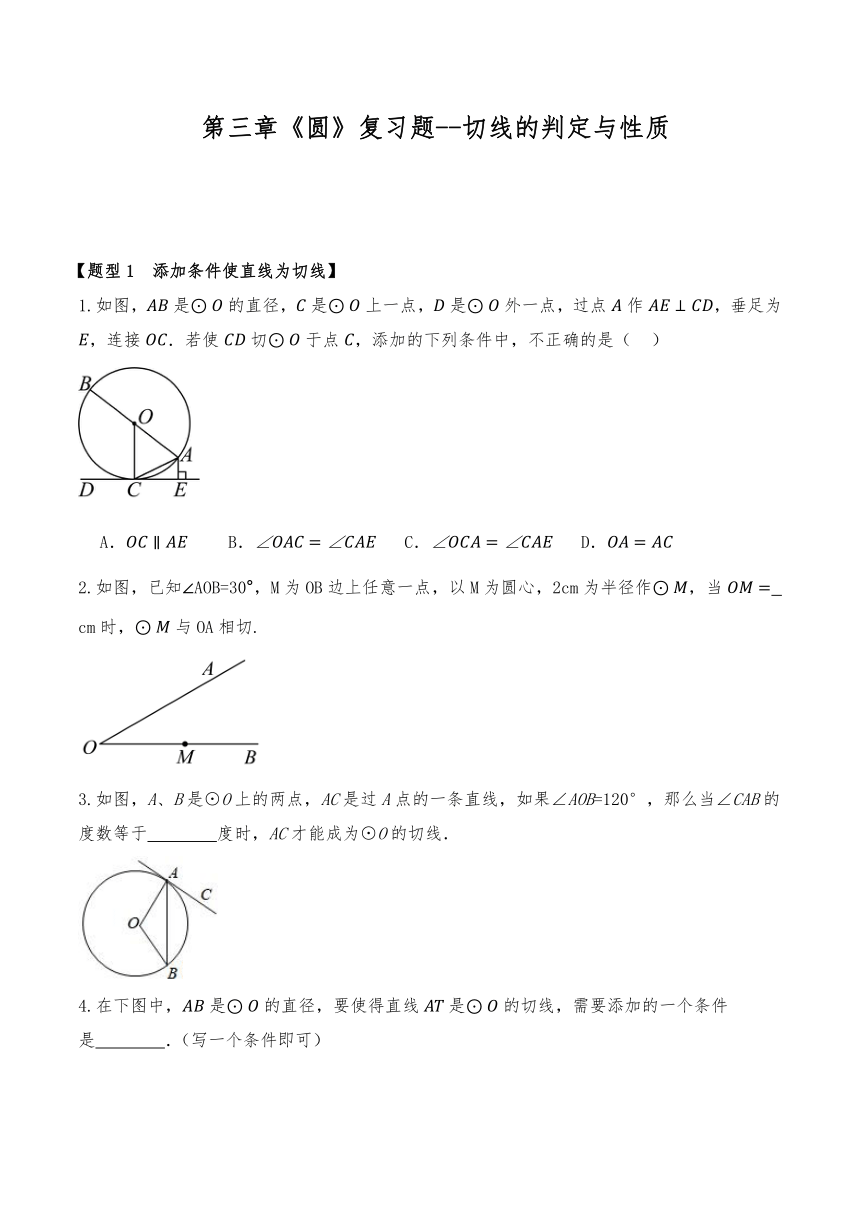
第三章《圆》复习题--切线的判定与性质 【题型1 添加条件使直线为切线】 1.如图,是的直径,是上一点,是外一点,过点作,垂足为,连接.若使切于点,添加的下列条件中,不正确的是( ) A. B. C. D. 2.如图,已知∠AOB=30°,M为OB边上任意一点,以M为圆心,2cm为半径作,当 cm时,与OA相切. 3.如图,A、B是⊙O上的两点,AC是过A点的一条直线,如果∠AOB=120°,那么当∠CAB的度数等于 度时,AC才能成为⊙O的切线. 4.在下图中,是的直径,要使得直线是的切线,需要添加的一个条件是 .(写一个条件即可) 【题型2 连半径证垂直证明是切线】 1.已知是的直径,点是延长线上一点,,是的弦,. (1)求证:直线是的切线; (2)若,垂足为,的半径为,求的长. 2.如图,将沿过点的直线翻折并展开,点的对应点落在边上,折痕为,点在边上,经过点、.若,判断与的位置关系,并说明理由. 3.如图,是的内接三角形,是的直径,为的中点,,在的延长线上. (1)是的切线吗?为什么? (2)若,则的度数为_____°. 4.如图1,为半圆的直径,点为圆心,为半圆的切线,过半圆上的点作交于点,连接. (1)连接,若,求证:是半圆的切线; (2)如图2,当线段与半圆交于点时,连接,,判断和的数量关系,并证明你的结论. 【题型3 作垂直证半径证明是切线】 1.如图,四边形中,,,,连接,以点B为圆心,长为半径作,交于点E. (1)试判断与的位置关系,并说明理由; (2)若,,求图中阴影部分的面积. 2.如图,O为正方形ABCD对角线上一点,以O为圆心,OA的长为半径的⊙O与CD相切于点M, (1)求证:BC与⊙O相切; (2)若正方形的边长为1,求⊙O的半径. 3.如图,在Rt△ABC中,∠B=90°,∠BAC的平分线交BC于点D,E为AB上的一点,DE=DC,以D为圆心,DB长为半径作⊙D,AB=5,EB=3. (1)求证:AC是⊙D的切线; (2)求线段AC的长. 4.如图1,为等腰三角形,是底边的中点,腰与⊙相切于点,底交于点,. (1)求证:是的切线; (2)如图2,连接,交于点,点是弧的中点,若,,求 的半径. 【题型4 由切线的性质求线段长度】 1.如图,是的内接三角形,.点是延长线上一点,且与相切于点,若的半径为1,则长为( ) A. B. C. D.3 2.如图,与相切于点A,交于点B,点C在上,且.若,,则的长为 . 3.如图,是⊙O的直径,,与⊙O相切于点A,交⊙O于点D,连接,若,则的长为( ) A.4 B. C.2 D. 4.如图,与相切于点,与弦相交于点,,若,,则的长为 . 【题型5 由切线的性质求角度】 1.如图,在中,,圆O与交于点D,与相切于点C,,则 . 2.如图,是的直径,,垂足为E,直线与相切于点C,交于点D,直线交的延长线于点P,连接,若,则的度数是( ) A. B. C. D. 3.如图,正六边形的边,与相切于点C,F,连接,,则的度数是( ) A.120° B.144° C.150° D.160° 4.如图分别切于A、B、E,,则( ) A. B. C. D. 【题型6 利用切线的性质进行证明】 1.如图,以的一边为直径作,点恰好落在上,射线与相切于点. (1)尺规作图:过点作于点,延长交于点,连接;(保留作图痕迹,标明相应字母,不写作法) (2)在(1)的条件下证明:. 2.如图,在中,,以为直径的交于点D,切线交于点E. (1)求证:; (2)若,,求的长. 3.如图,是的直径,是的一条弦,于点M,连接. (1)若,求的度数; (2)的延长线相交于点F,是的切线,交于点E,若,求证:. 4.如图,P为外一点,为的切线,切点分别为A、B,直线交于点D、E,交于点C. (1)求证∶. (2)若,连接,求证:四边形是菱形. 【题型7 作圆的切线】 1.如图,在每个小正方形的边长为1的网格中,的顶点A、B、C均落在格点上. (1)的周长为_____. (2)请在如图所示的网格中,用无刻 ... ...
~~ 您好,已阅读到文档的结尾了 ~~