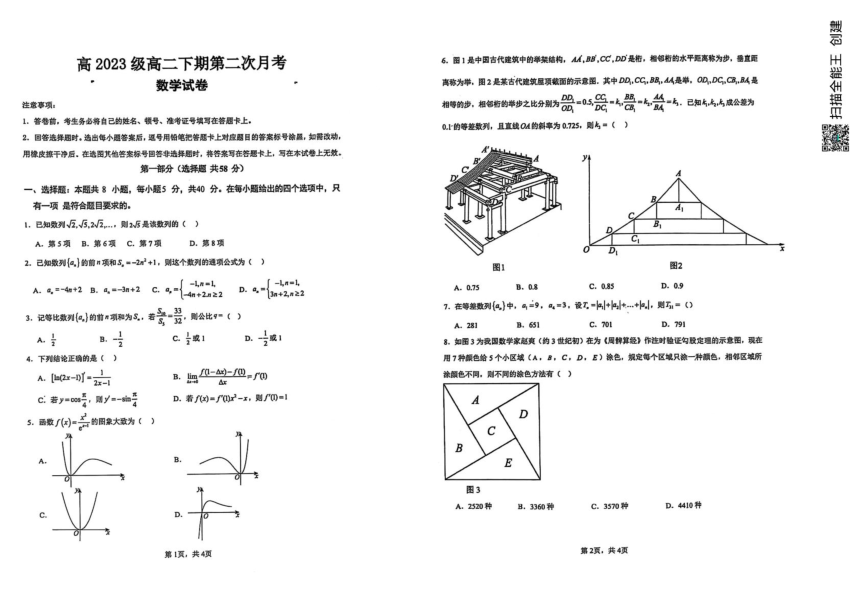
高2023级高二下期第二次月考 6.图1是中因古代建筑中的举架结构,A4,BB,CC,DD是桁,相邻析的水平距高称为步,舞直距 数学试卷 高称为举,图2是某古代建筑层顶鞍面的示意图.其中DD,CG,B8,4A是举,OD,DC,CB,BA是 注意事项: 相等的步,相部有的举岁之比分别为品=05瓷-乌器-与兰-大,已东片化5成公速为 1.答番前,考生务必将自己的姓名、顿号、准考证号填写在答题卡上, 0.r的等差数列,且直线04的斜率为0.725,则片=() 2。回答选择网时。选出每小题答案后,迅号用铅笔把答题卡上对应题目的答案标号涂属,如稀改动, 用橡皮接干净后。在选图其他答案标号回答非选择题时,艳答案写在答思卡上,写在本试卷上无效。 第一部分(选择题共58分) 一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只 有一项是符合题目要求的。 1.已知缴列V瓦,5,2W2,则25是该数列的() A.第5项B.第6项C.第7项D.第8项 0 D 2.己知数列{a}的前n项和5。■-2n+1,则这个数列的通项公式为() 图1 图2 [-l,n=1 A.a,=-4m+2B.4=-3n+2C.0{4m+2n22 -l,n=1 D.a,={3m+2,n22 A.0.75 B.0.8 C.0.85 D.09 3。记等比最列)的前0项和为8,若受-费。则公比9-() 7.在等差数列{a}中,4=9,a=3,设工=++…+,则工=() A,281 B.651 C.701 D.791 A支 B.月 C.或1 D.或1 8,如图3为我国数学家赵爽(约3世纪初)在为《周降算经》作注时验证勾股定理的示意图,现在 4.下列结论正确的是() 用7种颜色给5个小区域(A,B,C,D,E)涂色,规定每个区域只涂一种颜色,相邻区城所 A-=2 B.=--=fo 涂颜色不同,则不同的涂色方法有() △x C:若y=o经,则y=-血月 D.若f)=fQx2-x,则0=1 D 5.西数)=的图象大致为() B E 图3 A.2520种 B.3360种 C.3570种 D.4410种 第1页,共4页 第2页,共4页 器 二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项 符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分。 17.(15分)已知一企业生产某产品的年固定成本为10万元,每生产千件衙另投入2.7万元,若该 温 9.已知定义城为[-3,5]的函数∫(x)的导函致为'(x),且(x)的图象如图4所示,则() 企业二年内共生产此种产品x千件,并且全部销售完,每千件的销管收入为∫(x万元,且 08-动,00 C.的败∫(x)在x=2处取得极小值 D.的数∫(x)在x=3处取得极大值 ()泻出年利润W(万元)关于年产品x(千件)的函数解折式: 10.若函最/问-a血x+是+e0)既有极大值也有摄小值,则《人 (②)年产量为多少千件时,该企业生产此产品所获年利淘最大?最大利润是多少? A.be>0 B.ab>0 C.b2+8ac>0 (注:年利润=年销修收入年总成本) D.ac<0 11.己知函数∫()=-3到'+a-1,则下列选项正确的是() 8.(1)已知西数/)=xe-如-x(aeR。 A.y=f(x)在(2,3)上单调递减B.y=(x)恰有一个极大值 (0)若a=0,求f(x)的极小值:(2)当a>二时,求f()的单调递增区何: C.当a<1时,y=f()有三个零点D.当a=1时,U(x)=0有三个实数解 )当a>0时,设八倒的极大值为go),求证:g向)≥-是 第二部分(非选择题共92分) 三、空题:本题共3小题,每小题5分,共15分。 19.(17)英国数学家泰勘是18世纪早期一位非常杰出的数学家,以泰勒公式和泰勒级数闻名,泰 12.画线y血|x过坐标原点的两条切线的方程为 勒公式是数学分析的重要组成部分,它的理论方法在近似计算、求极限、不等式的证明停方面都有 13.将5个人排成一排,若甲和乙须排在一起,则有」 种不何的排法 重要的应用.例如:函数f(x)= 的带有佩亚诺余项的泰物展开式为: 14.已知定义在R上的函数(x)关于y轴对称,其导函数为(),当x之0时.不等式 ()+∫(x)>l.若对x∈R,不等式。f(c)-a时(ax)>o'-ar恒成立,则 ... ...
~~ 您好,已阅读到文档的结尾了 ~~