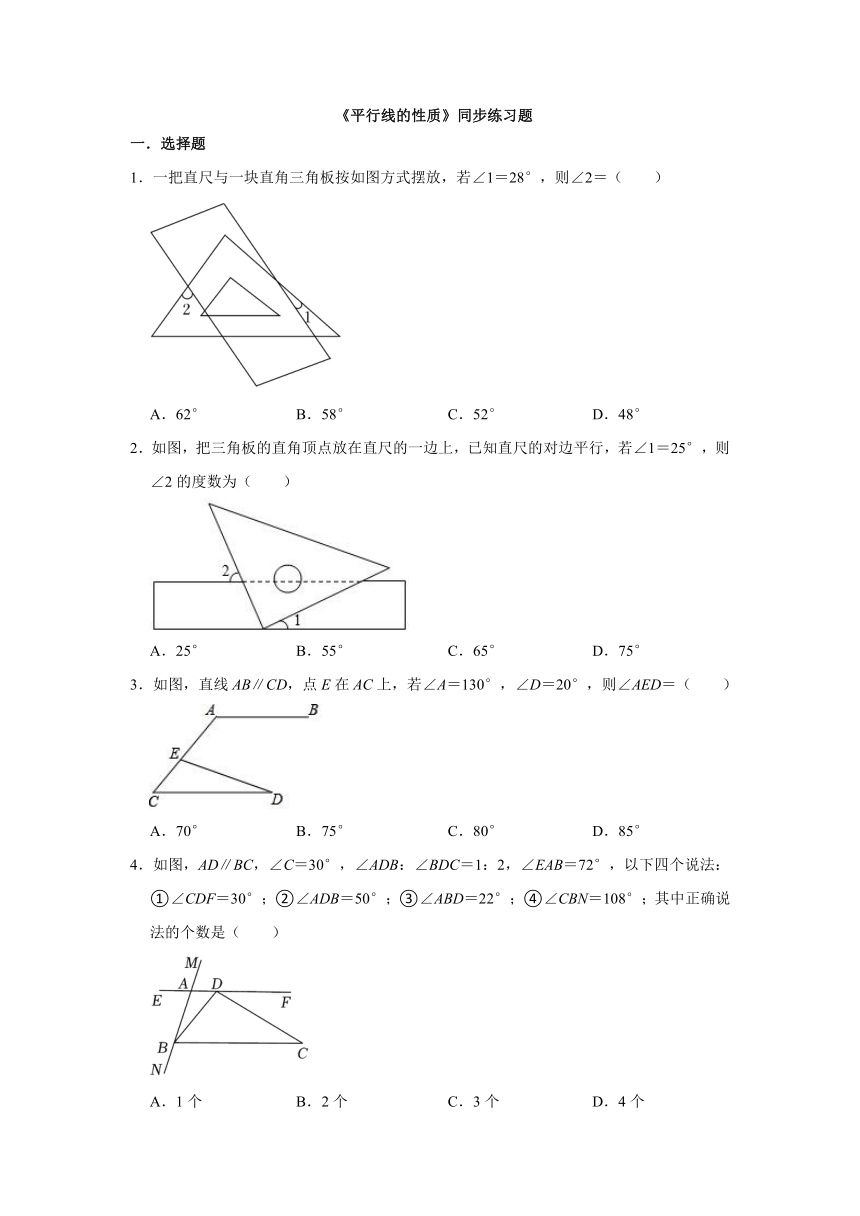
《平行线的性质》同步练习题 一.选择题 1.一把直尺与一块直角三角板按如图方式摆放,若∠1=28°,则∠2=( ) A.62° B.58° C.52° D.48° 2.如图,把三角板的直角顶点放在直尺的一边上,已知直尺的对边平行,若∠1=25°,则∠2的度数为( ) A.25° B.55° C.65° D.75° 3.如图,直线AB∥CD,点E在AC上,若∠A=130°,∠D=20°,则∠AED=( ) A.70° B.75° C.80° D.85° 4.如图,AD∥BC,∠C=30°,∠ADB:∠BDC=1:2,∠EAB=72°,以下四个说法: ①∠CDF=30°;②∠ADB=50°;③∠ABD=22°;④∠CBN=108°;其中正确说法的个数是( ) A.1个 B.2个 C.3个 D.4个 5.如图,在△DEF中,点C在DF的延长线上,点B在EF上,且AB∥CD,∠EBA=60°,则∠E+∠D的度数为( ) A.60° B.30° C.90° D.80° 6.如图,将一张长方形纸带沿EF折叠,点C、D的对应点分别为C'、D'.若∠DEF=α,用含α的式子可以将∠C'FG表示为( ) A.2α B.90°+α C.180°﹣α D.180°﹣2α 7.如图,AB∥CD,∠FGB=155°,FG平分∠EFD,则∠AEF的大小为( ) A.25° B.50° C.70° D.77.5° 8.如图,一条公路经过两次转弯后又回到原来的方向,如果第一次的拐角为150°,则第二次的拐角为( ) A.40° B.50° C.140° D.150° 二.填空题 9.如图,∠AOB内有一点P,过点P画PC∥OB,PD∥OA,∠AOB=60°,则∠CPD的度数为 度. 10.如图,DE∥BC,CD平分∠ACB,∠ACB=58°,则∠EDC= . 11.如图,a∥b,∠1=30°,∠2=90°,则∠3的度数是 . 12.如图,将长方形纸条ABCD沿EF折叠,使得点A落在点G处,点B落在点H处,已知∠1=70°,则∠2= . 13.如图,把一条两边边沿互相平行的纸带折叠,若∠β=56°,则∠α= . 三.解答题 14.完成下面的证明. 如图,直线a⊥b,b∥c.求证a⊥c. 证明:∵a⊥b(已知), ∴∠1= ( ). ∵b∥c( ), ∴∠1= ( ). ∴∠2=∠1= ( ). ∴a⊥c( ). 15.如图,已知AB∥DC,AC⊥BC,AC平分∠DAB,∠B=50°,求∠D的大小. 阅读下面的解答过程,并填括号里的空白(理由或数学式). 解:∵AB∥DC( ), ∴∠B+∠DCB=180°( ). ∵∠B= (已知), ∴∠DCB=180°﹣∠B=180°﹣50°=130°. ∵AC⊥BC(已知), ∴∠ACB= (垂直的定义). ∴∠2= . ∵AB∥DC(已知), ∴∠1= ( ). ∵AC平分∠DAB(已知), ∴∠DAB=2∠1= (角平分线的定义). ∵AB∥DC(已知), ∴ +∠DAB=180°(两条直线平行,同旁内角互补). ∴∠D=180°﹣∠DAB= . 16.如图,AB∥CD,∠BAC 的角平分线AP与∠ACD的角平分线CP相交于点P. 求证:AP⊥CP. 17.平面内的两条直线有相交和平行两种位置关系. (1)如图1,若AB∥CD,点P在AB、CD内部,∠B=50°,∠D=30°,求∠BPD的度数; (2)如图2,在AB∥CD的前提下,将点P移到AB、CD外部,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论; (3)如图3,写出∠BPD、∠B、∠D、∠BQD之间的数量关系?(不需证明); (4)如图4,计算∠A+∠B+∠C+∠D+∠E+∠F的度数是 . 18.当光线经过镜面反射时,入射光线、反射光线与镜面所夹的角对应相等.例如:在图①、图②中,都有∠1=∠2,∠3=∠4.设镜子AB与BC的夹角∠ABC=α. (1)如图①,若α=90°,∠1=50°,则∠4= °; (2)如图②,若α=115°,入射光线EF与反射光线GH的夹角∠FMH=β.求β的度数; (3)如图③,若90°<α<180°,设镜子CD与BC的夹角∠BCD=γ(90°<γ<180 ... ...
~~ 您好,已阅读到文档的结尾了 ~~

